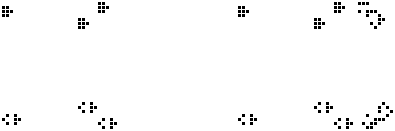B35/S236

Glider Logic

We can build logic circuits out of several elements: guns to create constant-one signals; vanishing reactions used as "a and not b" gates (which are sufficient to build up all other boolean formulas); eaters to delete stray gliders; turns to connect and resynchronize signal paths; and two-to-one or two-to-two glider reactions to copy signals.

The only remaining ingredient for universality is some kind of memory. Dean suggests a sliding block memory, based on reactions in which glider salvos push or pull a block two squares:

3 gliders push a block 2 units 4 gliders pull a block 2 units

To detect a block in the zero position, we shoot a glider at it:

glider removes a block

If the glider disappears we know the block was at zero; we then rebuild the block using a head-on collision:

2 gliders form a block

I prefer a delay line memory to a sliding block, for reasons of computational efficiency. The best version of this I've been able to set up involves reflecting salvos of gliders off the back of a pair of c/3 spaceships:

glider packets reflect from a c/3 spaceship

One could instead base a delay line on a reaction with the c/5 spaceship that turns a glider into a block, but that would require more careful synchronization.

These all haven't been put together into an explicit universal computer, but I think it should be clear that such a computer exists.

B35/S236 -- Cellular Automata -- D. Eppstein -- UCI Inf. & Comp. Sci.