|
Files |
| file | vfetk.h |
| | Contains declarations for class Vfetk.
|
Data Structures |
| struct | sVfetk |
| | Contains public data members for Vfetk class/module. More...
|
| struct | sVfetk_LocalVar |
| | Vfetk LocalVar subclass Contains variables used when solving the PDE with FEtk. More...
|
Typedefs |
|
typedef enum eVfetk_LsolvType | Vfetk_LsolvType |
| | Declare FEMparm_LsolvType type.
|
|
typedef enum eVfetk_NsolvType | Vfetk_NsolvType |
| | Declare FEMparm_NsolvType type.
|
|
typedef enum eVfetk_GuessType | Vfetk_GuessType |
| | Declare FEMparm_GuessType type.
|
|
typedef enum eVfetk_PrecType | Vfetk_PrecType |
| | Declare FEMparm_GuessType type.
|
|
typedef sVfetk_LocalVar | Vfetk_LocalVar |
| | Declaration of the Vfetk_LocalVar subclass as the Vfetk_LocalVar structure.
|
|
typedef sVfetk | Vfetk |
| | Declaration of the Vfetk class as the Vfetk structure.
|
Enumerations |
| enum | eVfetk_LsolvType {
VLT_SLU = 0,
VLT_MG = 1,
VLT_CG = 2,
VLT_BCG = 3
} |
| | Linear solver type. More...
|
| enum | eVfetk_NsolvType {
VNT_NEW = 0,
VNT_INC = 1,
VNT_ARC = 2
} |
| | Non-linear solver type. More...
|
| enum | eVfetk_GuessType {
VGT_ZERO = 0,
VGT_DIRI = 1,
VGT_PREV = 2
} |
| | Initial guess type. More...
|
| enum | eVfetk_PrecType {
VPT_IDEN = 0,
VPT_DIAG = 1,
VPT_MG = 2
} |
| | Preconditioner type. More...
|
Functions |
| Gem * | Vfetk_getGem (Vfetk *thee) |
| | Get a pointer to the Gem (grid manager) object.
|
| AM * | Vfetk_getAM (Vfetk *thee) |
| | Get a pointer to the AM (algebra manager) object.
|
| Vpbe * | Vfetk_getVpbe (Vfetk *thee) |
| | Get a pointer to the Vpbe (PBE manager) object.
|
| Vcsm * | Vfetk_getVcsm (Vfetk *thee) |
| | Get a pointer to the Vcsm (charge-simplex map) object.
|
| int | Vfetk_getAtomColor (Vfetk *thee, int iatom) |
| | Get the partition information for a particular atom.
|
| Vfetk * | Vfetk_ctor (Vpbe *pbe, Vhal_PBEType type) |
| | Constructor for Vfetk object.
|
| int | Vfetk_ctor2 (Vfetk *thee, Vpbe *pbe, Vhal_PBEType type) |
| | FORTRAN stub constructor for Vfetk object.
|
| void | Vfetk_dtor (Vfetk **thee) |
| | Object destructor.
|
| void | Vfetk_dtor2 (Vfetk *thee) |
| | FORTRAN stub object destructor.
|
| double * | Vfetk_getSolution (Vfetk *thee, int *length) |
| | Create an array containing the solution (electrostatic potential in units of 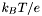 ) at the finest mesh level. ) at the finest mesh level.
|
| void | Vfetk_setParameters (Vfetk *thee, PBEparm *pbeparm, FEMparm *feparm) |
| | Set the parameter objects.
|
| double | Vfetk_energy (Vfetk *thee, int color, int nonlin) |
| | Return the total electrostatic energy.
|
| double | Vfetk_dqmEnergy (Vfetk *thee, int color) |
| | Get the "mobile charge" and "polarization" contributions to the electrostatic energy.
|
| double | Vfetk_qfEnergy (Vfetk *thee, int color) |
| | Get the "fixed charge" contribution to the electrostatic energy.
|
| unsigned long int | Vfetk_memChk (Vfetk *thee) |
| | Return the memory used by this structure (and its contents) in bytes.
|
| void | Vfetk_setAtomColors (Vfetk *thee) |
| | Transfer color (partition ID) information frmo a partitioned mesh to the atoms.
|
| void | Bmat_printHB (Bmat *thee, char *fname) |
| | Writes a Bmat to disk in Harwell-Boeing sparse matrix format.
|
| int | Vfetk_genCube (Vfetk *thee, double center[VAPBS_DIM], double length[VAPBS_DIM]) |
| | Generates a simple cubic tetrahedral mesh.
|
| PDE * | Vfetk_PDE_ctor (Vfetk *fetk) |
| | Constructs the FEtk PDE object.
|
| int | Vfetk_PDE_ctor2 (PDE *thee, Vfetk *fetk) |
| | Intializes the FEtk PDE object.
|
| void | Vfetk_PDE_dtor (PDE **thee) |
| | Destroys FEtk PDE object.
|
| void | Vfetk_PDE_dtor2 (PDE *thee) |
| | FORTRAN stub: destroys FEtk PDE object.
|
| void | Vfetk_PDE_initAssemble (PDE *thee, int ip[], double rp[]) |
| | Do once-per-assembly initialization.
|
| void | Vfetk_PDE_initElement (PDE *thee, int elementType, int chart, double tvx[][VAPBS_DIM], void *data) |
| | Do once-per-element initialization.
|
| void | Vfetk_PDE_initFace (PDE *thee, int faceType, int chart, double tnvec[]) |
| | Do once-per-face initialization.
|
| void | Vfetk_PDE_initPoint (PDE *thee, int pointType, int chart, double txq[], double tU[], double tdU[][VAPBS_DIM]) |
| | Do once-per-point initialization.
|
| void | Vfetk_PDE_Fu (PDE *thee, int key, double F[]) |
| | Evaluate strong form of PBE. For interior points, this is:
![\[ -\nabla \cdot \epsilon \nabla u + b(u) - f \]](form_61.png)
where 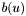 is the (possibly nonlinear) mobile ion term and is the (possibly nonlinear) mobile ion term and 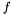 is the source charge distribution term (for PBE) or the induced surface charge distribution (for RPBE). For an interior-boundary (simplex face) point, this is: is the source charge distribution term (for PBE) or the induced surface charge distribution (for RPBE). For an interior-boundary (simplex face) point, this is:
![\[ [\epsilon(x) \nabla u(x) \cdot n(x)]_{x=0^+} - [\epsilon(x) \nabla u(x) \cdot n(x)]_{x=0^-} \]](form_64.png)
where 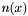 is the normal to the simplex face and the term represents the jump in dielectric displacement across the face. There is no outer-boundary contribution for this problem. is the normal to the simplex face and the term represents the jump in dielectric displacement across the face. There is no outer-boundary contribution for this problem.
|
| double | Vfetk_PDE_Fu_v (PDE *thee, int key, double V[], double dV[][VAPBS_DIM]) |
| | This is the weak form of the PBE; i.e. the strong form integrated with a test function to give:
![\[ \int_\Omega \left[ \epsilon \nabla u \cdot \nabla v + b(u) v - f v \right] dx \]](form_66.png)
where 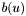 denotes the mobile ion term. denotes the mobile ion term.
|
| double | Vfetk_PDE_DFu_wv (PDE *thee, int key, double W[], double dW[][VAPBS_DIM], double V[], double dV[][VAPBS_DIM]) |
| | This is the linearization of the weak form of the PBE; e.g., for use in a Newton iteration. This is the functional linearization of the strong form integrated with a test function to give:
![\[ \int_\Omega \left[ \epsilon \nabla w \cdot \nabla v + b'(u) w v - f v \right] dx \]](form_67.png)
where 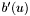 denotes the functional derivation of the mobile ion term. denotes the functional derivation of the mobile ion term.
|
| void | Vfetk_PDE_delta (PDE *thee, int type, int chart, double txq[], void *user, double F[]) |
| | Evaluate a (discretized) delta function source term at the given point.
|
| void | Vfetk_PDE_u_D (PDE *thee, int type, int chart, double txq[], double F[]) |
| | Evaluate the Dirichlet boundary condition at the given point.
|
| void | Vfetk_PDE_u_T (PDE *thee, int type, int chart, double txq[], double F[]) |
| | Evaluate the "true solution" at the given point for comparison with the numerical solution.
|
| void | Vfetk_PDE_bisectEdge (int dim, int dimII, int edgeType, int chart[], double vx[][VAPBS_DIM]) |
| | Define the way manifold edges are bisected.
|
| void | Vfetk_PDE_mapBoundary (int dim, int dimII, int vertexType, int chart, double vx[VAPBS_DIM]) |
| | Map a boundary point to some pre-defined shape.
|
| int | Vfetk_PDE_markSimplex (int dim, int dimII, int simplexType, int faceType[VAPBS_NVS], int vertexType[VAPBS_NVS], int chart[], double vx[][VAPBS_DIM], void *simplex) |
| | User-defined error estimator -- in our case, a geometry-based refinement method; forcing simplex refinement at the dielectric boundary and (for non-regularized PBE) the charges.
|
| void | Vfetk_PDE_oneChart (int dim, int dimII, int objType, int chart[], double vx[][VAPBS_DIM], int dimV) |
| | Unify the chart for different coordinate systems -- a no-op for us.
|
| double | Vfetk_PDE_Ju (PDE *thee, int key) |
| | Energy functional. This returns the energy (less delta function terms) in the form:
![\[ c^{-1}/2 \int (\epsilon (\nabla u)^2 + \kappa^2 (cosh u - 1)) dx \]](form_69.png)
for a 1:1 electrolyte where 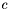 is the output from Vpbe_getZmagic. is the output from Vpbe_getZmagic.
|
| void | Vfetk_externalUpdateFunction (SS **simps, int num) |
| | External hook to simplex subdivision routines in Gem. Called each time a simplex is subdivided (we use it to update the charge-simplex map).
|
| int | Vfetk_PDE_simplexBasisInit (int key, int dim, int comp, int *ndof, int dof[]) |
| | Initialize the bases for the trial or the test space, for a particular component of the system, at all quadrature points on the master simplex element.
|
| void | Vfetk_PDE_simplexBasisForm (int key, int dim, int comp, int pdkey, double xq[], double basis[]) |
| | Evaluate the bases for the trial or test space, for a particular component of the system, at all quadrature points on the master simplex element.
|
| void | Vfetk_readMesh (Vfetk *thee, int skey, Vio *sock) |
| | Read in mesh and initialize associated internal structures.
|
| void | Vfetk_dumpLocalVar () |
| | Debugging routine to print out local variables used by PDE object.
|
| int | Vfetk_fillArray (Vfetk *thee, Bvec *vec, Vdata_Type type) |
| | Fill an array with the specified data.
|
| int | Vfetk_write (Vfetk *thee, const char *iodev, const char *iofmt, const char *thost, const char *fname, Bvec *vec, Vdata_Format format) |
| | Write out data.
|
|
|
Initialize the bases for the trial or the test space, for a particular component of the system, at all quadrature points on the master simplex element.
- Author:
- Mike Holst
- Note:
* The basis ordering is important. For a fixed quadrature
* point iq, you must follow the following ordering in p[iq][],
* based on how you specify the degrees of freedom in dof[]:
*
* <v_0 vDF_0>, <v_1 vDF_0>, ..., <v_{nv} vDF_0>
* <v_0 vDF_1>, <v_1 vDF_1>, ..., <v_{nv} vDF_1>
* ...
* <v_0 vDF_{nvDF}>, <v_0 vDF_{nvDF}>, ..., <v_{nv} vDF_{nvDF}>
*
* <e_0 eDF_0>, <e_1 eDF_0>, ..., <e_{ne} eDF_0>
* <e_0 eDF_1>, <e_1 eDF_1>, ..., <e_{ne} eDF_1>
* ...
* <e_0 eDF_{neDF}>, <e_1 eDF_{neDF}>, ..., <e_{ne} eDF_{neDF}>
*
* <f_0 fDF_0>, <f_1 fDF_0>, ..., <f_{nf} fDF_0>
* <f_0 fDF_1>, <f_1 fDF_1>, ..., <f_{nf} fDF_1>
* ...
* <f_0 fDF_{nfDF}>, <f_1 fDF_{nfDF}>, ..., <f_{nf} fDF_{nfDF}>
*
* <s_0 sDF_0>, <s_1 sDF_0>, ..., <s_{ns} sDF_0>
* <s_0 sDF_1>, <s_1 sDF_1>, ..., <s_{ns} sDF_1>
* ...
* <s_0 sDF_{nsDF}>, <s_1 sDF_{nsDF}>, ..., <s_{ns} sDF_{nsDF}>
*
* For example, linear elements in R^3, with one degree of freedom at each *
* vertex, would use the following ordering:
*
* <v_0 vDF_0>, <v_1 vDF_0>, <v_2 vDF_0>, <v_3 vDF_0>
*
* Quadratic elements in R^2, with one degree of freedom at each vertex and
* edge, would use the following ordering:
*
* <v_0 vDF_0>, <v_1 vDF_0>, <v_2 vDF_0>
* <e_0 eDF_0>, <e_1 eDF_0>, <e_2 eDF_0>
*
* You can use different trial and test spaces for each component of the
* elliptic system, thereby allowing for the use of Petrov-Galerkin methods.
* You MUST then tag the bilinear form symmetry entries as nonsymmetric in
* your PDE constructor to reflect that DF(u)(w,v) will be different from
* DF(u)(v,w), even if your form acts symmetrically when the same basis is
* used for w and v.
*
* You can also use different trial spaces for each component of the elliptic
* system, and different test spaces for each component of the elliptic
* system. This allows you to e.g. use a basis which is vertex-based for
* one component, and a basis which is edge-based for another. This is
* useful in fluid mechanics, eletromagnetics, or simply to play around with
* different elements.
*
* This function is called by MC to build new master elements whenever it
* reads in a new mesh. Therefore, this function does not have to be all
* that fast, and e.g. could involve symbolic computation.
*
- Parameters:
-
| dim |
Basis type to evaluate (0 = trial, 1 = test, 2 = trialB, 3 = testB) |
| comp |
Spatial dimension |
| ndof |
Which component of elliptic system to produce basis for? |
| dof |
Set to the number of degrees of freedom Set to degree of freedom per v/e/f/s |
|
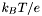 ) at the finest mesh level.
) at the finest mesh level. ![\[ -\nabla \cdot \epsilon \nabla u + b(u) - f \]](form_61.png)
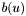 is the (possibly nonlinear) mobile ion term and
is the (possibly nonlinear) mobile ion term and 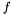 is the source charge distribution term (for PBE) or the induced surface charge distribution (for RPBE). For an interior-boundary (simplex face) point, this is:
is the source charge distribution term (for PBE) or the induced surface charge distribution (for RPBE). For an interior-boundary (simplex face) point, this is: ![\[ [\epsilon(x) \nabla u(x) \cdot n(x)]_{x=0^+} - [\epsilon(x) \nabla u(x) \cdot n(x)]_{x=0^-} \]](form_64.png)
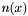 is the normal to the simplex face and the term represents the jump in dielectric displacement across the face. There is no outer-boundary contribution for this problem.
is the normal to the simplex face and the term represents the jump in dielectric displacement across the face. There is no outer-boundary contribution for this problem. ![\[ \int_\Omega \left[ \epsilon \nabla u \cdot \nabla v + b(u) v - f v \right] dx \]](form_66.png)
![\[ \int_\Omega \left[ \epsilon \nabla w \cdot \nabla v + b'(u) w v - f v \right] dx \]](form_67.png)
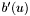 denotes the functional derivation of the mobile ion term.
denotes the functional derivation of the mobile ion term. ![\[ c^{-1}/2 \int (\epsilon (\nabla u)^2 + \kappa^2 (cosh u - 1)) dx \]](form_69.png)
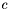 is the output from Vpbe_getZmagic.
is the output from Vpbe_getZmagic. ![\[ G = \frac{1}{4 I_s} \sum_i c_i q_i^2 \int \overline{\kappa}^2(x) e^{-q_i u(x)} dx + \frac{1}{2} \int \epsilon ( \nabla u )^2 dx \]](form_59.png)
![\[ G = \frac{1}{2} \int \overline{\kappa}^2(x) u^2(x) dx + \frac{1}{2} \int \epsilon ( \nabla u )^2 dx \]](form_60.png)
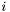 denotes the counterion species,
denotes the counterion species, 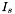 is the bulk ionic strength,
is the bulk ionic strength, 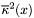 is the modified Debye-Huckel parameter,
is the modified Debye-Huckel parameter, 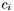 is the concentration of species
is the concentration of species 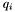 is the charge of species
is the charge of species 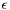 is the dielectric function, and
is the dielectric function, and 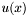 is the dimensionless electrostatic potential. The energy is scaled to units of
is the dimensionless electrostatic potential. The energy is scaled to units of 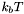 .
.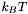 .
. ![\[ G = \sum_i q_i u(r_i) \]](form_11.png)
 1.3.5
1.3.5