Polyhedra and Polytopes

• Adventures among the toroids. Reference to a book on polyhedral tori by B. M. Stewart.

• Archimedean solids: John Conway describes some interesting maps among the Archimedean polytopes. Eric Weisstein lists properties and pictures of the Archimedean solids.

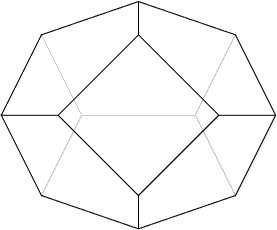
• Associahedron and Permutahedron. The associahedron represents the set of triangulations of a hexagon, with edges representing flips; the permutahedron represents the set of permutations of four objects, with edges representing swaps. This strangely asymmetric view of the associahedron (as an animated gif) shows that it has some kind of geometric relation with the permutahedron: it can be formed by cutting the permutahedron on two planes. A more symmetric view is below. See also a more detailed description of the associahedron and Jean-Louis Loday's paper on associahedron coordinates.
  

• David Bailey's world of tesselations. Primarily consists of Escher-like drawings but also includes an interesting section about Kepler's work on polyhedra.

• Ned Batchelder's Stellated Dodecahedron T-shirt.

• The bellows conjecture, R. Connelly, I. Sabitov and A. Walz in Contributions to Algebra and Geometry , volume 38 (1997), No.1, 1-10. Connelly had previously discovered non-convex polyhedra which are flexible (can move through a continuous family of shapes without bending or otherwise deforming any faces); these authors prove that in any such example, the volume remains constant throughout the flexing motion.

• Bounded degree triangulation. Pankaj Agarwal and Sandeep Sen ask for triangulations of convex polytopes in which the vertex or edge degree is bounded by a constant or polylog.

• Buckyballs. The truncated icosahedron recently acquired new fame and a new name when chemists discovered that Carbon forms molecules with its shape.

• The charged particle model: polytopes and optimal packing of p points in n dimensional spheres.

• Circumnavigating a cube and a tetrahedron, Henry Bottomley.

• Cognitive Engineering Lab, Java applets for exploring tilings, symmetry, polyhedra, and four-dimensional polytopes.

• Complex polytope. A diagram representing a complex polytope, from H. S. M. Coxeter's home page.

• a computational approach to tilings. Daniel Huson investigates the combinatorics of periodic tilings in two and three dimensions, including a classification of the tilings by shapes topologically equivalent to the five Platonic solids.

• Convex Archimedean polychoremata, 4-dimensional analogues of the semiregular solids, described by Coxeter-Dynkin diagrams representing their symmetry groups.

• A Counterexample to Borsuk's Conjecture, J. Kahn and G. Kalai, Bull. AMS 29 (1993). Partitioning certain high-dimensional polytopes into pieces with smaller diameter requires a number of pieces exponential in the dimension.

• Deltahedra, polyhedra with equilateral triangle faces. From Eric Weisstein's treasure trove of mathematics.

• Dodecafoam. A fractal froth of polyhedra fills space.

• Dodecahedron measures, Paul Kunkel.

• Domegalomaniahedron. Clive Tooth makes polyhedra out of his deep and inscrutable singular name.

• Explore the 120-cell! Free Windows+OpenGL+.Net software.

• All the fair dice. Pictures of the polyhedra which can be used as dice, in that there is a symmetry taking any face to any other face.

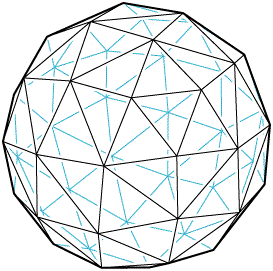
• Chris Fearnley's 5 and 25 Frequency Geodesic Spheres rendered by POV-Ray.

• Five Platonic solids and a soccerball.

• Five space-filling polyhedra. And not the ones you're likely thinking of, either. Guy Inchbald, reproduced from Math. Gazette 80, November 1996.

• Flexible polyhedra. From Dave Rusin's known math pages.

• The Fourth Dimension. John Savard provides a nice graphical explanation of the four-dimensional regular polytopes.

• Four-dimensional visualization. Doug Zare gives some pointers on high-dimensional visualization including a description of an interesting chain of successively higher dimensional polytopes beginning with a triangular prism.

• Geodesic math. Apparently this means links to pages about polyhedra.

• Geometria Java-based software for constructing and measuring polyhedra by transforming and slicing predefined starting blocks.

• Geometry, algebra, and the analysis of polygons. Notes by M. Brundage on a talk by B. Grünbaum on vector spaces formed by planar n-gons under componentwise addition.

• Geometry and the Imagination in Minneapolis. Notes from a workshop led by Conway, Doyle, Gilman, and Thurston. Includes several sections on polyhedra, knots, and symmetry groups.

• Glowing green rhombic triacontahedra in space. Rendered by Rob Wieringa for the May-June 1997 Internet Ray Tracing Competition.

• The golden section and Euclid's construction of the dodecahedron, and more on the dodecahedron and icosahedron, H. Serras, Ghent.

• Polyhedra - homage to U. A. Graziotti.

• Great triambic icosidodecahedron quilt, made by Mark Newbold and Sarah Mylchreest with the aid of Mark's hyperspace star polytope slicer.

• Melinda Green's geometry page. Green makes models of regular sponges (infinite non-convex generalizations of Platonic solids) out of plastic "Polydron" pieces.

• Hebesphenomegacorona onna stick in space! Space Station Science picture of the day. In case you don't remember what a hebesphenomegacorona is, it's one of the Johnson solids: convex polyhedra with regular-polygon faces.

• Hecatohedra. John Conway discusses the possible symmetry groups of hundred-sided polyhedra.
  

• Hilbert's 3rd Problem and Dehn Invariants. How to tell whether two polyhedra can be dissected into each other. See also Walter Neumann's paper connecting these ideas with problems of classifying manifolds.

• Holyhedra. Jade Vinson solves a question of John Conway on the existence of finite polyhedra all of whose faces have holes in them (the Menger sponge provides an infinite example).

• HypArr, software for modeling and visualizing convex polyhedra and plane arrangements, now seems to be incorporated as a module in a larger Matlab library for multi-parametric analysis.

• Hypergami polyhedral playground. Rotatable wireframe models of platonic solids and of the penguinhedron.

• Hyperspace star polytope slicer, Java animation by Mark Newbold.
  

• The icosahedron, the great icosahedron, graph designs, and Hadamard matrices. Notes by M. Brundage from a talk by M. Rosenfeld.

• Icosamonohedra, icosahedra made from congruent but not necessarily equilateral triangles.

• Ideal hyperbolic polyhedra ray-traced by Matthias Weber.

• Guy Inchbald's polyhedra pages. Stellations, hendecahedra, duality, space-fillers, quasicrystals, and more.

• The International Bone-Roller's Guild ponders the isohedra: polyhedra that can act as fair dice, because all faces are symmetric to each other.

• Investigating Patterns: Symmetry and Tessellations. Companion site to a middle school text by Jill Britton, with links to many other web sites involving symmetry or tiling.

• Jenn open-source software for visualizing Cayley graphs of Coxeter groups as symmetric 4-dimensional polytopes.

• Johnson Solids, convex polyhedra with regular faces. From Eric Weisstein's treasure trove of mathematics.

• Sándor Kabai's mathematical graphics, primarily polyhedra and 3d fractals.

• Kepler-Poinsot Solids, concave polyhedra with star-shaped faces. From Eric Weisstein's treasure trove of mathematics. See also H. Serras' page on Kepler-Poinsot solids.

• Links2go: Polyhedra
  

• Louis Bel's povray galleries: les polyhèdres réguliers, knots, and more knots.

• Lunatic's guide to polyhedra.

• 3-Manifolds from regular solids. Brent Everitt lists the finite volume orientable hyperbolic and spherical 3-manifolds obtained by identifying the faces of regular solids.

• Maple polyhedron gallery.

• Martin's pretty polyhedra. Simulation of particles repelling each other on the sphere produces nice triangulations of its surface.

• Mathematica Graphics Gallery: Polyhedra

• Max. non-adjacent vertices on 120-cell. Sci.math discussion on the size of the maximum independent set on this regular 4-polytope. Apparently it is known to be between 220 and 224 inclusive.

• Minesweeper on Archimedean polyhedra, Robert Webb.

• Models of Platonic solids and related symmetric polyhedra.

• Netlib polyhedra. Coordinates for regular and Archimedean polyhedra, prisms, anti-prisms, and more.

• Nine. Drew Olbrich discovers the associahedron by evenly spacing nine points on a sphere and dualizing.

• Nonorthogonal polyhedra built from rectangles. Melody Donoso and Joe O'Rourke answer an open question of Biedl, Lubiw, and Sun.
  

• Occult correspondences of the Platonic solids. Some random thoughts from Anders Sandberg.

• Pappus on the Archimedean solids. Translation of an excerpt of a fourth century geometry text.

• Peek, software for visualizing high-dimensional polytopes.

• Penumbral shadows of polygons form projections of four-dimensional polytopes. From the Graphics Center's graphics archives.

• Pictures of 3d and 4d regular solids, R. Koch, U. Oregon. Koch also provides some 4D regular solid visualization applets.

• The Platonic solids. With Java viewers for interactive manipulation. Peter Alfeld, Utah.

• Platonic solids and Euler's formula. Vishal Lama shows how the formula can be used to show that the familiar five Platonic solids are the only ones possible.

• Platonic solids and quaternion groups, J. Baez.

• Platonic solids transformed by Michael Hansmeyer using subdivision-surface algorithms into shapes resembling radiolarans. See also Boing Boing discussion.

• Platonic spheres. Java animation, with a discussion of platonic solid classification, Euler's formula, and sphere symmetries.

• Platonic Universe, Stephan Werbeck. What shapes can you form by gluing regular dodecahedra face-to-face?

• Poly, Windows/Mac shareware for exploring various classes of polyhedra including Platonic solids, Archimedean solids, Johnson solids, etc. Includes perspective views, Shlegel diagrams, and unfolded nets.

• Polygonal and polyhedral geometry. Dave Rusin, Northern Illinois U.

• Polygons as projections of polytopes. Andrew Kepert answers a question of George Baloglou on whether every planar figure formed by a convex polygon and all its diagonals can be formed by projecting a three-dimensional convex polyhedron.

• Polygons, polyhedra, polytopes, R. Towle.

• Polyhedra. Bruce Fast is building a library of images of polyhedra. He describes some of the regular and semi-regular polyhedra, and lists names of many more including the Johnson solids (all convex polyhedra with regular faces).

• Polyhedra collection, V. Bulatov.

• Polyhedra exhibition. Many regular-polyhedron compounds, rendered in povray by Alexandre Buchmann.

• Polyhedra pastimes, links to teaching activities collected by J. Britton.

• A polyhedral analysis. Ken Gourlay looks at the Platonic solids and their stellations.

• Polyhedron, polyhedra, polytopes, ... - Numericana.

• Polyhedron challenge: cuboctahedron.

• Polyhedron web scavenger hunt

• PolyGloss. Wendy Krieger is unsatisfied with terminology for higher dimensional geometry and attempts a better replacement. Her geometry works include some other material on higher dimensional polytopes.

• Polytope movie page. GIF animations by Komei Fukuda.

• Proofs of Euler's Formula. V-E+F=2, where V, E, and F are respectively the numbers of vertices, edges, and faces of a convex polyhedron.

• Puzzles by Eric Harshbarger, mostly involving colors of and mazes on polyhedra and polyominoes.

• Puzzles with polyhedra and numbers, J. Rezende. Some questions about labeling edges of platonic solids with numbers, and their connections with group theory.

• The Puzzling World of Polyhedral Dissections. Stewart T. Coffin's classic book on geometric puzzles, now available in full text on the internet!

• Quark constructions. The sun4v.qc Team investigates polyhedra that fit together to form a modular set of building blocks.

• A quasi-polynomial bound for the diameter of graphs of polyhedra, G. Kalai and D. Kleitman, Bull. AMS 26 (1992). A famous open conjecture in polyhedral combinatorics (with applications to e.g. the simplex method in linear programming) states that any two vertices of an n-face polytope are linked by a chain of O(n) edges. This paper gives the weaker bound O(n^{log d}).

• Realization Spaces of 4-polytopes are Universal, G. Ziegler and J. Richter-Gebert, Bull. AMS 32 (1995).

• Regular polyhedra as intersecting cylinders. Jim Buddenhagen exhibits ray-traces of the shapes formed by extending half-infinite cylinders around rays from the center to each vertex of a regular polyhedron. The boundary faces of the resulting unions form combinatorially equivalent complexes to those of the dual polyhedra.

• Regular polytopes in higher dimensions. Russell Towle uses Mathematica to slice and dice simplices, hypercubes, and the other high-dimensional regular polytopes. See also Russell's 4D star polytope quicktime animations.
  

• Regular polytopes in Hilbert space. Dan Asimov asks what the right definition of such a thing should be.

• Regular solids. Information on Schlafli symbols, coordinates, and duals of the five Platonic solids. (This page's title says also Archimedean solids, but I don't see many of them here.)

• Resistance and conductance of polyhedra. Derek Locke computes formulae for networks of unit resistors in the patterns of the edges of the Platonic solids. See also the section on resistors in the rec.puzzles faq.

• Rhombic spirallohedra, concave rhombus-faced polyhedra that tile space, R. Towle.

• Rolling polyhedra. Dave Boll investigates Hamiltonian paths on (duals of) regular polyhedra.

• Ruler and Compass. Mathematical web site including special sections on the geometry of polyhedrons and geometry of polytopes.

• The Simplex: Minimal Higher Dimensional Structures. D. Anderson.

• Simplex/hyperplane intersection. Doug Zare nicely summarizes the shapes that can arise on intersecting a simplex with a hyperplane: if there are p points on the hyperplane, m on one side, and n on the other side, the shape is (a projective transformation of) a p-iterated cone over the product of m-1 and n-1 dimensional simplices.

• Six-regular toroid. Mike Paterson asks whether it is possible to make a torus-shaped polyhedron in which exactly six equilateral triangles meet at each vertex.

• SMAPO library of polytopes encoding the solutions to optimization problems such as the TSP.

• Soap bubble 120-cell from the Geometry Center archives.
  

• Solution of Conway-Radin-Sadun problem. Dissections of combinations of regular dodecahedra, regular icosahedra, and related polyhedra into rhombs that tile space. By Dehn's solution to Hilbert's third problem this is impossible for individual dodecahedra and icosahedra, but Conway, Radin, and Sadun showed that certain combinations could work. Now Izidor Hafner shows how.

• Squares are not diamonds. Izzycat gives a nice explanation of why these shapes should be thought of differently, even though they're congruent: they generalize to different things in higher dimensions.

• Stella and Stella4d, Windows software for visualizing regular and semi-regular polyhedra and their stellations in three and four dimensions, morphing them into each other, drawing unfolded nets for making paper models, and exporting polyhedra to various 3d design packages.

• Stellations of the dodecahedron stereoscopically animated in Java by Mark Newbold.

• Sterescopic polyhedra rendered with POVray by Mark Newbold.

• The Story of the 120-cell, John Stillwell, Notices of the AMS. History, algebra, geometry, topology, and computer graphics of this regular 4-dimensional polytope.

• Structors. Panagiotis Karagiorgis thinks he can get people to pay large sums of money for exclusive rights to use four-dimensional regular polytopes as building floor plans. But he does have some pretty pictures...

• Student of Hyperspace. Pictures of 6 regular polytopes, E. Swab.

• Superliminal Geometry. Topics include deltahedra, infinite polyhedra, and flexible polyhedra.

• Symmetries of torus-shaped polyhedra

• Symmetry, tilings, and polyhedra, S. Dutch.

• Synergetic geometry, Richard Hawkins' digital archive. Animations and 3d models of polyhedra and tensegrity structures. Very bandwidth-intensive.

• The Szilassi Polyhedron. This polyhedral torus, discovered by L. Szilassi, has seven hexagonal faces, all adjacent to each other. It has an axis of 180-degree symmetry; three pairs of faces are congruent leaving one unpaired hexagon that is itself symmetric. Tom Ace has more images as well as a downloadable unfolded pattern for making your own copy. See also Dave Rusin's page on polyhedral tori with few vertices and Ivars' Peterson's MathTrek article.
  

• Tales of the dodecahedron, from Pythagoras to Plato to Poincaré. John Baez, Reese Prosser Memorial Lecture, Dartmouth, 2006.

• 3D-Geometrie. T. E. Dorozinski provides a gallery of images of 3d polyhedra, 2d and 3d tilings, and subdivisions of curved surfaces.

• Three dimensional turtle talk description of a dodecahedron. The dodecahedron's description is "M40T72R5M40X63.435T288X296.565R5M40T72M40X63.435T288X296.565R4"; isn't that helpful?

• Three untetrahedralizable objects

• Triangles and squares. Slides from a talk I gave relating a simple 2d puzzle, Escher's drawings of 3d polyhedra, and the combinatorics of 4d polytopes, via angles in hyperbolic space. Warning: very large file (~8Mb). For more technical details see my paper with Kuperberg and Ziegler.
  

• Truncated Octahedra. Hop David has a nice picture of Coxeter's regular sponge {6,4|4}, formed by leaving out the square faces from a tiling of space by truncated octahedra.

• Truncated Trickery: Truncatering. Some truncation relations among the Platonic solids and their friends.

• Tuvel's Polyhedra Page and Tuvel's Hyperdimensional Page. Information and images on universal polyhedra and higher dimensional polytopes.

• Two-distance sets. Timothy Murphy and others discuss how many points one can have in an n-dimensional set, so that there are only two distinct interpoint distances. The correct answer turns out to be n²/2 + O(n). This talk abstract by Petr Lisonek (and paper in JCTA 77 (1997) 318-338) describe some related results.

• Uniform polychora. A somewhat generalized definition of 4d polytopes, investigated and classified by J. Bowers, the polyhedron dude. See also the dude's pages on 4d polytwisters and 3d uniform polyhedron nomenclature.

• Uniform polyhedra. Computed by Roman Maeder using a Mathematica implementation of a method of Zvi Har'El. Maeder also includes separately a picture of the 20 convex uniform polyhedra, and descriptions of the 59 stellations of the icosahedra.

• Uniform polyhedra in POV-ray format, by Russell Towle.
  

• Uniform polyhedra, R. Morris. Rotatable 3d java view of these polyhedra.

• An uninscribable 4-regular polyhedron. This shape can not be drawn with all its vertices on a single sphere.
  

• Variations of Uniform Polyhedra, Vince Matsko.

• Visual techniques for computing polyhedral volumes. T. V. Raman and M. S. Krishnamoorthy use Zome-based ideas to derive simple expressions for the volumes of the Platonic solids and related shapes.

• Visualization of the Carrillo-Lipman Polytope. Geometry arising from the simultaneous comparison of multiple DNA or protein sequences.

• Volumes in synergetics. Volumes of various regular and semi-regular polyhedra, scaled according to inscribed tetrahedra.

• Volumes of ideal hyperbolic hypercubes.

• Volumes of pieces of a dodecahedron. David Epstein (not me!) wonders why parallel slices through the layers of vertices of a dodecahedron produce equal-volume chunks.

• Waterman polyhedra, formed from the convex hulls of centers of points near the origin in an alternating lattice. See also Paul Bourke's Waterman Polyhedron page.
  

• Why doesn't Pick's theorem generalize? One can compute the volume of a two-dimensional polygon with integer coordinates by counting the number of integer points in it and on its boundary, but this doesn't work in higher dimensions.

• Why "snub cube"? John Conway provides a lesson on polyhedron nomenclature and etymology. From the geometry.research archives.

• Zonohedra and zonotopes. These centrally symmetric polyhedra provide another way of understanding the combinatorics of line arrangements.

From the Geometry Junkyard, computational and recreational geometry pointers.
Send email if you know of an appropriate page not listed here.
David Eppstein, Theory Group, ICS, UC Irvine.
Semi-automatically filtered from a common source file.