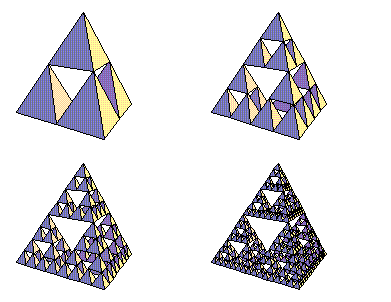
Sierpinski Tetrahedra and Other Fractal Sponges
This seems to be everyone's favorite three-dimensional fractal, so much
so that I've had to add a separate page for it and several other closely
related fractals. The Sierpinski Tetrahedron has Hausdorff dimension
two, so maybe it's not really a fractal in the "fractional dimension"
sense of the word. It can be formed in many ways: (1) start with a
single tetrahedron and remove octahedra from it, (2) recursively combine
quadruples of tetrahedra into larger tetrahedra, (3) take "Pascal's
Pyramid" of trinomial coefficients modulo two, (4) form the graph of the
binary exclusive-or function on the unit square. The last construction shows
that if you look down on it from the right direction, it just looks like
a square, but from other viewpoints it has plenty of holes, so it can
form a sort of "Venetian blind" that casts shadows only in certain
directions.
- Animation of the
fast Fourier transform of a Menger Sponge.
- ASCII Menger sponge, W. Taylor.
- The business card Menger
sponge project. Jeannine Mosely wants to build a fractal cube out of
66048 business cards. The MIT Origami Club has already made a smaller version of the same shape.
- Deconstructing
Marty. Tom Beard and Dorking Labs
analyze the Sierpinski-carpet-like geometry of New Zealand fractal
artist Martin Thompson's works.
- Sylvie Donmoyer
geometry-inspired paintings including Menger sponges and
a behind-the-scenes look at Escher's Stars.
- The
fractal gallery tour: Sierpinski tetrahedron
- Fractal
skewed web. Sierpinski tetrahedron by Mary Ann Conners.
- Fractals by da duke.
Ray-traced Menger sponges and Sierpinski gaskets.
- Fun with Fractals and
the Platonic Solids. Gayla Chandler places models of polyhedra and
polyhedral fractals such as the Sierpinski tetrahedron in scenic outdoor
settings and photographs them there.
- IFS and L-systems.
Vittoria Rezzonico grows fractal broccoli and Sierpinski pyramids.
- Interactive
fractal polyhedra, Evgeny Demidov.
- Making a Sierpinski pyramid with Maple, S. Sutherland, Stony Brook.
- Mathematica
Menger Sponge, Robert M. Dickau.
- Mengermania!
- Menger
Cubes, Peter C. Miller.
Including some animated ray traces and a discussion of eliminating
irrelevant internal surfaces prior to rendering.
- Menger sponge
floating in space. Everyone and his brother makes ray-traced
fractals with unlikely backgrounds nowadays, but Cliff Pickover was
there first.
- Origami
Menger Sponge
built from Sonobe modules by K. & W. Burczyk.
- Paperforms.
John Vonachen uses laser cutters and spray paint to make and sell paper
models of polyhedra, stellated
polyhedra, polyhedral complexes, Sierpinski tetrahedra, etc.
- Project
X. "a shape that is homogenized, saturated with equalities, inanely
geometric, yet also irresolvable, paradoxical, UNHEALTHY"
- Rainbow
Sierpinski tetrahedron by Aécio de Féo Flora Neto.
- Rubik's Cube
Menger Sponge, Hana Bizek.
- Santa Rosa
Menger Cube made by Tom Falbo and helpers at Santa Rosa Junior College
from 8000 1-inch-cubed oak blocks.
- Sierpinski
cookies. Actually more like Menger cookies, but whatever.
- Sierpinski
gaskets and Menger sponges, Paul Bourke.
Including stacks of coke cans, radio antennas, crumpled sponges, and more.
- Sierpinski Hamantaschen.
- Sierpinski gaskets and variations rendered by D. H. Hepting.
- Sierpinski
pentatope video by Chris Edward Dupilka. A four-dimensional analogue
of the Sierpinski triangle.
- Sierpinski pyramid.
C++ code for generating the Sierpinski tetrahedron.
- Sierpinski
tetrahedron. Awful Mathematica code used by Robert Dickau to
generate the following sequence of images.
- Sierpinski
tetrahedron animation (MS-video format), Karl S. Frederickson.
- Sierpinski triangle reptile
based on a complex binary number system, R. W. Gosper.
- Sierpinski valentine from XKCD.
- Tetrahedral
kite. A. Thyssen describes how to make Sierpinski tetrahedra out of
soda straws, kite strings, and plastic shopping bags.
- Tetrix. From Eric Weisstein's treasure trove.
- Tune's polyhedron models.
Sierpinski octahedra, stellated icosahedra, interlocking
zonohedron-dissection puzzles, and more.
- Visualising
fractals in 3D. Sierpinski tetrahedron in Stonehenge, and a Menger sponge.
- What
is David Fowler making a Sierpinski tetrahedron out of? It looks
like toothpicks and marshmallows, or maybe pieces of styrofoam peanuts.
- What to make with golf balls? Dale Seymour chooses a Sierpinski triangle and Sierpinski tetrahedron.
From the Geometry Junkyard,
computational
and recreational geometry pointers.
Send email if you
know of an appropriate page not listed here.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Semi-automatically
filtered
from a common source file.