Diffusion Distance

Diffusion Distance Definition

We generalize the diffusion distance defined by Hammond et al. (Hammond, Gur, and Johnson 2013). This distortion measure between two undirected graphs $G_1$ and $G_2$, of the same size, was defined as: $$\begin{aligned} D_{\text{Hammond}} (G_1, G_2) = \sup_{t} { \left| \left| e^{t L_1} - e^{t L_2} \right| \right| }_F^2 \end{aligned}$$ where $L_i$ represents the graph Laplacian of $G_i$. A typical example of this distance, as $t$ is varied, can be seen in Figure [fig:hammond_distance].

[fig:hammond_distance]

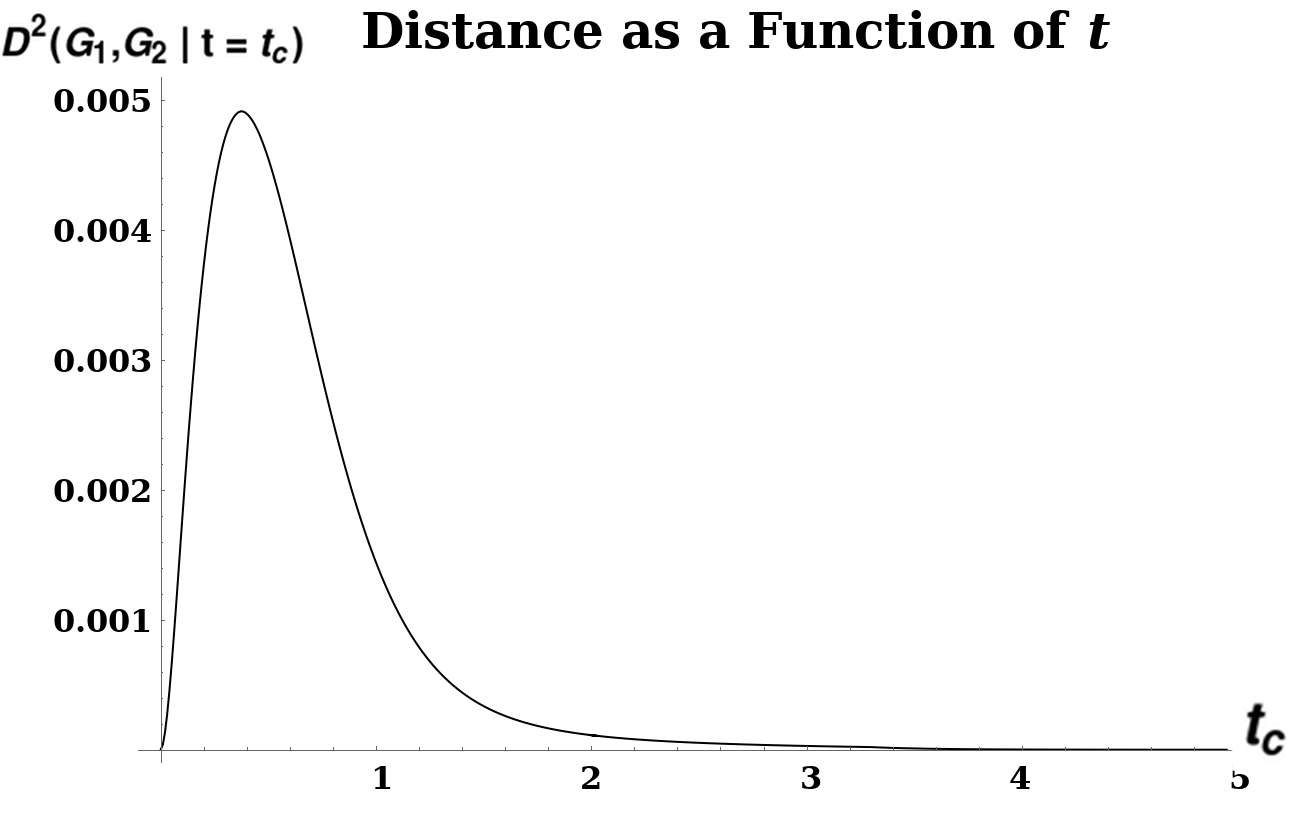
[fig:typical_ham_dist]

This may be interpreted as measuring the maximum divergence, as a function of $t$, between diffusion processes starting from each vertex of each graph, as measured by the squared Euclidean distance between the column vectors of $e^{t L_i}$. Each column $v_j$ of $e^{t L_i}$ (which is called the Laplacian Exponential Kernel) describes a probability distribution of visits (by a random walk of duration $t$, with node transition probabilities given by the columns of $e^L$) to the vertices of $G_i$, starting at vertex $j$. This distance metric is then measuring the difference between the two graphs by comparing these probability distributions; the motivation between taking the supremum over all $t$ is that the value of the objective function at the maximum is the most these two distributions can diverge. See Figure [fig:typical_ham_dist] for an example of a distance calculation, with a characteristic peak.

For further intuition about why the peak is the most natural place to take as the distance, rather than some other arbitrary time, note that at very early times and very late times, the probability distribution of vertex visits is agnostic to graph structure: at early times no diffusion has had a chance to take place, while at very late times the distribution of vertex-visits converges to the stationary state1 for each connected component of the graph. Hence we are most interested in a regime of $t$-values in between these extremes, where differences in $G_1$ and $G_2$ are apparent in their differing probability distributions.

Our contribution generalizes this measure to allow for graphs of differing size. We add two variables to this optimization: a prolongation operator, $P$ (represented as a rectangular matrix), and a time-scaling factor, $\alpha$. The dissimilarity between two graphs $G_1$ and $G_2$ (with Laplacians $L_i = L(G_i)$) is then defined as: $$\begin{aligned} \label{defn:exp_defn} D^2(G_1,G_2) &= \sup_{t>0} \inf_{\alpha > 0} \inf_{P | \mathcal{C}(P)} {\left| \left| P e^{\frac{t}{\alpha} L_1} - e^{\alpha t L_2} P \right| \right|}^2_F \end{aligned}$$ where $\mathcal{C}(P)$ represents some set of constraints on the matrix $P$. For the remainder of this work we use $D(G_1,G_2)$ to refer to the distance and $D^2(G_1,G_2)$ to refer to the squared distance - this notation is chosen to simplify the exposition of some proofs. It will be convenient for later calculations to introduce and assume the concept of transitive constraints - by which we mean that for any constraint $\mathcal{C}$, satisfaction of $\mathcal{C}$ by $P_1$ and $P_2$ implies satisfaction of $\mathcal{C}$ by their product $P_1 P_2$ (when such a product is defined). Some (non-exclusive) examples of transitive constraints include orthogonality, particular forms of sparsity, and their conjunctions.

The simplest transitive constraint we will consider is that $P$ should be orthogonal. Intuitively, an orthogonal $P$ represents a norm-preserving map between nodes of $G_1$ and nodes of $G_2$, so we are measuring how well diffusion on $G_1$ approximates diffusion on $G_2$, as projected by $P$. Note that since in general $P$ is a rectangular matrix it is not necessarily true that $P P^T = I$. We assume that $\left| G_1\right| = n_1 \leq n_2 = \left| G_2 \right|$; if not, the order of the operands is switched, so that $P$ is always at least as tall as it is wide. We also briefly consider a sparsity constraint in Section 3.4 below. Since sparsity is more difficult to treat numerically, our default constraint will be orthogonality alone. Other constraints could include bandedness and other structural constraints. We also note that because $L$ is finite-dimensional, the exponential map is continuous and therefore we can swap the order of optimization over $t$ and $\alpha$. The optimization procedure outlined in this thesis optimizes these variables in the order presented above (namely: an outermost loop of maximization over $t$, a middle loop of minimization over $\alpha$ given $t$, and an innermost loop of minimization over $P$ given $t$ and $\alpha$).

The other additional parameter, $\alpha$, controls dilation between the passage of time in the two graphs, to account for different scales. Again, the intuition is that we are interested in the difference between structural properties of the graph (from the point of view of single-particle diffusion) independent of the absolute number of nodes in the graph. As an example, diffusion on an $n \times n$ grid is a reasonably accurate approximation of more rapid diffusion on a $2n \times 2n$ grid, especially when $n$ is very large. In our discussion of variants of this dissimilarity score, we will use the notation $D^2(G_1, G_2 | x = c)$ to mean restrictions of any of our distortion measure equations where variable $x$ is held to a constant value $c$; In cases where it is clear from context which variable is held to a fixed value $c$, we will write $D^2(G_1, G_2 | c)$

At very early times the second and higher-order terms of the Taylor Series expansion of the matrix exponential function vanish, and so $e^{t L} \approx I + t L$. This motivates the early-time or “linear” version of this distance, $\tilde{D}$: $$\begin{aligned} \label{defn:linear_defn} \tilde{D}^2(G_1,G_2) &= \inf_{\alpha > 0} \inf_{P | \mathcal{C}(P)} {\left| \left| \frac{1}{\alpha} P L_1 - \alpha L_2 P \right| \right|}^2_F \\ &\approx \frac{1}{t^2} \left( \inf_{\alpha > 0} \inf_{P | \mathcal{C}(P)} {\left| \left| P e^{\frac{t}{\alpha} L_1} - e^{\alpha t L_2} P \right| \right|}^2_F \right) \end{aligned}$$

(Note that the identity matrices cancel). The outermost optimization (maximization over $t$) is removed for this version of the distance, as $t$ can be factored out:

$$\begin{aligned} {\left| \left| \frac{t}{\alpha} P L_1 - \alpha t L_2 P \right| \right|}^2_F = t^2 {\left| \left| \frac{1}{\alpha} P L_1 - \alpha L_2 P \right| \right|}^2_F \end{aligned}$$

This means that for the linear version, we only optimize $\alpha$ and $P$. For the exponential version of the dissimilarity score, we note briefly that the supremum over $t$ of our objective function must exist, since for any $G_1, G_2$: $$\begin{aligned} \label{eqn:D_limit_1} D^2(G_1, G_2) \leq D^2 \left(G_1, G_2 \left| \alpha = 1, P= \left[ \begin{array}{c} I \\ 0 \end{array}\right] \right. \right) \end{aligned}$$ In other words, the infimum over all $P$ and $\alpha$ is bounded above by any particular choice of values for these variables. Since $$\begin{aligned} \label{eqn:D_limit_2} D^2 &\left(G_1, G_2 \left| t = 0, \alpha = 1, P = \left[ \begin{array}{c} I \\ 0 \end{array}\right] \right. \right) = 0 , & \text{and} \\ \lim_{t_c \rightarrow \infty} D^2 & \left(G_1, G_2 \left| t_c, \alpha = 1, P= \left[ \begin{array}{c} I \\ 0 \end{array}\right] \right. \right) = 0 \end{aligned}$$ this upper bound must have a supremum (possibly 0) at some $t^* \in [ 0, \infty)$. Then $$\begin{aligned} D^2 \left(G_1, G_2 \left| t^*, \alpha = 1, P = \left[ \begin{array}{c} I \\ 0 \end{array}\right] \right. \right) \end{aligned}$$ must be finite and therefore so must the objective function.

Directedness of Distance and Constraints

We note that this distance measure, as defined so far, is directed: the operands $G_1$ and $G_2$ serve differing roles in the objective function. This additionally makes the constraint predicate $\mathcal{C}(P)$ ambiguous: when we state that $\mathcal{C}$ represents orthogonality, it is not clear whether we are referring to $P ^T P = I$ or $P P ^T = I$ (only one of which can be true for a non-square matrix $P$). To remove this ambiguity, we will, for the computations in the rest of this manuscript, define the distance metric to be symmetric: the distance between $G_1$ and $G_2$ with $\left| G_1 \right| \leq \left| G_2 \right|$ is always $D(G_1, G_2)$. $P$ is then always at least as tall as it is wide, so of the two choices of orthogonality constraint we select $P ^T P = I$.

Variants of Distance Measure

Thus far we have avoided referring to this graph dissimilarity function as a “distance metric”. As we shall see later, full optimization of Equations [defn:exp_defn] and [defn:linear_defn] over $\alpha$ and $P$ is too loose, in the sense that the distances $D(G_1, G_2)$, $D(G_2, G_3)$, and $D(G_1, G_3)$ do not necessarily satisfy the triangle inequality. The same is true for $\tilde{D}$. See Section 5.3 for numerical experiments suggesting a particular parameter regime where the triangle inequality is satisfied. We thus define several restricted/augmented versions of both $D$ and $\tilde{D}$ which are guaranteed to satisfy the triangle inequality. These different versions are summarized in Table [tab:dist_versions]. These variously satisfy some of the conditions necessary for generalized versions of distance metrics, including:

• Premetric: a function $d(x,y)$ for which $d(x,y) \geq 0$ and $d(x,y) = d(y,x)$ for all $x,y$.

• Pseudometric: As a premetric, but additionally $d(x,z) \leq d(x,y) + d(y,z)$ for all $x, y, z$.

• $\rho$-inframetric: As a premetric, but additionally $d(x,z) \leq \rho \left(d(x,y) + d(y,z)\right)$ and $d(x,y) = 0$ if and only if $x=y$, for all $x, y, z$.

Additionally, we note here that a distance measure on graphs using Laplacian spectra can at best be a pseudometric, since isospectral, non-isomorphic graphs are well-known to exist (Godsil and McKay 1982)(Van Dam and Haemers 2003). Characterizing the conditions under which two graphs are isospectral but not isomorphic is an open problem in spectral graph theory. However, previous computational work has led to the conjecture that “almost all” graphs are uniquely defined by their spectra (Brouwer and Haemers 2011)(Brouwer and Spence 2009)(Van Dam and Haemers 2009), in the sense that the probability of two graphs of size $n$ being isospectral but not isomorphic goes to 0 as $n \rightarrow \infty$. Furthermore, our numerical experiments seem to show empirically that the violation of the triangle inequality is bounded, in the sense that $D(G_1, G_3) \leq \rho * \left(D(G_1, G_2) + D(G_2, G_3) \right)$ for $\rho \approx 2.1$. This means that even in the least restricted case our similarity measure may be a $2.1$-infra-pseudometric on graphs (and, since such isospectral, non-isomorphic graphs are relatively rare, it behaves like a $2.1-$inframetric). As we will see in Chapter 3, in some more restricted cases we can prove triangle inequalities, making our measure a pseudometric. In Section 4.1, we discuss an algorithm for computing the optima in Equations ([defn:exp_defn]) and ([defn:linear_defn]). First, we discuss some theoretical properties of this dissimilarity measure.

Spectral Lower Bound

In Theorem [thm:LAP_bound] of Chapter 4 we will derive and make use of an upper bound on the graph distance $\tilde{D}(G_1, G_2)$. This upper bound is calculated by constraining the variable $P$ to be not only orthogonal, but also $P = U_2 M U_1^T$ where $M$ is the solution (i.e. “matching”, in the terminology of that section) to a Linear Assignment problem with costs given by a function of the eigenvalues of $L(G_1)$ and $L(G_2)$. In this section we derive a similar lower bound on the distance.

Let $G_1$ and $G_2$ be undirected graphs with Laplacians $L_1 = L(G_1)$ and $L_2 = L(G_2)$, and let $\alpha > 0$ be constant. By Equation [eqn:simple_d_tilde], we have

$$\begin{aligned} \tilde{D}^2(G_1,G_2) &= \inf_{\alpha > 0} \inf_{P^T P = I} \left( \sum\limits_{i=1}^{n_2}\sum\limits_{j=1}^{n_1} p_{ij}^2 {\left( \frac{1}{\alpha} {\lambda^{(1)}_j} - \alpha {\lambda^{(2)}_i} \right)}^2 \right). \end{aligned}$$ The following upper bound on $\tilde{D}$ is achieved by constraining $P$ to be not only orthogonal, but related to a constrained matching problem between the two lists of eigenvalues:

$$\label{eqn:upper_bound_2_defn} \begin{array}{ll@{}ll} \tilde{D}^2(G_1,G_2) \leq \inf_{\alpha>0} \inf_{M} & {\left| \left| \frac{1}{\alpha} M \Lambda_1 - \alpha \Lambda_2 M \right| \right|}^2_F &\\ \text{subject to}& \displaystyle\sum\limits_{i=1}^{n_2} m_{ij} \leq 1, &j=1 \ldots n_1\\ & \displaystyle\sum\limits_{j=1}^{n_1} m_{ij} \leq 1, &i=1 \ldots n_2\\ & m_{ij} \geq 0 & i = 1 \ldots n_2, j = 1 \ldots n_1, \\ \end{array}$$ where $\Lambda_1$ and $\Lambda_2$ are diagonal matrices of the eigenvalues of $L_1$ and $L_2$ respectively. Here we used the explicit map $\tilde{P} = U_2^T P U_1$ as a change of basis; we then converted the constraints on $P$ into equivalent constraints on $\tilde{P}$, and imposed additional constraints so that the resulting optimization (a linear assignment problem) is an upper bound. See the proof of Theorem [thm:LAP_bound] for the details of this derivation. We show in this section that a less constrained assignment problem is a lower bound on $\tilde{D}^2$. We do this by computing the same mapping $\tilde{P} = U_2^T P U_1$ and then dropping some of the constraints on $\tilde{P}$ (which is equivalent to dropping constraints on $P$, yielding a lower bound). The constraint $P^T P = I$ is the conjunction of $n_1 ^ 2$ constraints on the column vectors of $P$: if $\mathbf{p}_i$ is the $i$th column of $P$, then $P^T P = I$ is equivalent to: $$\begin{aligned} \mathbf{p}_i \cdot \mathbf{p}_i = 1 & \qquad & \forall i=1 \ldots n_1 \label{eqn:p_const_l1}\\ \mathbf{p}_i \cdot \mathbf{p}_i = 0 & \qquad & \forall i = 1 \ldots n_1, j = 1 \ldots i-1, i+1 \ldots n_1, \label{eqn:p_const_l2} \end{aligned}$$ If we discard the constraints in Equation [eqn:p_const_l2], we are left with the constraint that every column of $p$ must have unit norm.

Construct the “spectral lower bound matching” matrix $P^{(\text{SLB})}$ as follows:

$$P^{(\text{SLB})}_{i,j} = \begin{cases} 1 & \text{if i = } \arg \min_k {\left( \frac{1}{\alpha} \lambda^{(1)}_j - \alpha \lambda^{(k)}_k \right)}^2 \\ 0 & \text{otherwise.} \end{cases}$$ For any $\alpha$, this matrix is the solution to a matching problem (less constrained than the original optimization over all $P$) where each $\lambda^{(1)}_j$ is assigned to the closest $\lambda^{(2)}_i$, allowing collisions. It clearly satisfies the constraints in Equation [eqn:p_const_l1], but may violate those in Equation [eqn:p_const_l2]. Thus, we have

$$\begin{aligned} \tilde{D}^2(G_1,G_2) &= \inf_{\alpha > 0} \inf_{P^T P = I} \left( \sum\limits_{i=1}^{n_2}\sum\limits_{j=1}^{n_1} p_{ij}^2 {\left( \frac{1}{\alpha} {\lambda^{(1)}_j} - \alpha {\lambda^{(2)}_i} \right)}^2 \right). \\ &\geq \tilde{D}^2\left(G_1,G_2 \left| P^{(\text{SLB})} \right.\right) \end{aligned}$$

Various algorithms exist to rapidly find the member of a set of points which is closest to some reference point (for example, KD-Trees (Bentley 1975)). For any $\alpha$, the spectral lower bound can be calculated by an outer loop over alpha and an inner loop which applies one of these methods. We do not consider joint optimization of the lower bound over $P$ and $\alpha$ in this work.

Summary of Distance Metric Versions

Table [tab:dist_versions] summarizes the variants of our distance metric.

[tab:dist_versions]