Collection Classes: Final Issues (Hash Tables)

Introduction to Computer Science II
ICS-22

Introduction This lecture will cover a few remaining topics that are useful to know when dealing with collection classes in Java. First, we will examine the class named Collections (plural, not the interface named Collection), which like the Arrays class provides many useful static methods that operate on collections (take collections as parameters).

Second we will briefly discuss hashing; we will learn just enough so that we can get the general feel for how it works in principle: why all its operations are O(1), why we should not mutate a hashed value, etc. We will examine how various classes write their hashCode methods and discuss how to write this method for our own classes.

Finally, we will briefly examine Java 1.5's mechanism for writing generic collections (to avoid casting and have the compiler check more things before running our programs). This mechanism is very powerful: in simple cases it is straightforwardly useful, but beyond that its use is very interesting and can become much more subtle. The next lecture note covers this topic in more detail.

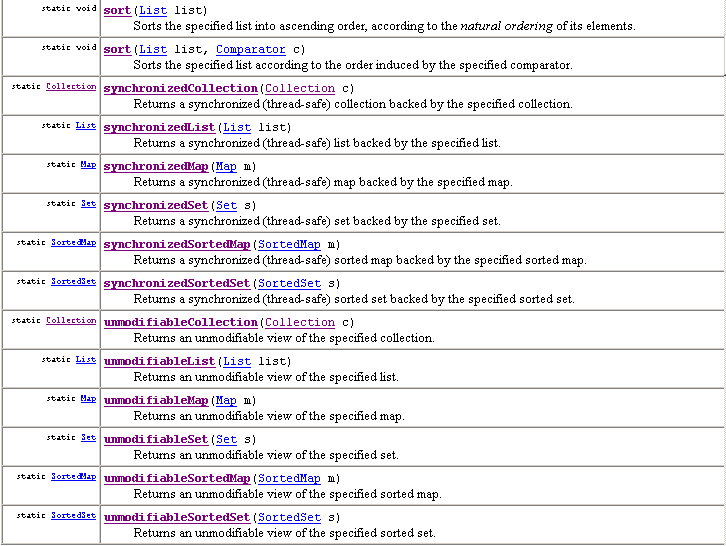
The Collections Class The Collections class is a library of various useful static methods that have collection classes (those implementing the Collection (singular) interface or its subinterfaces) as their parameters. The Javadoc summary of its methods appears below, and is discussed next.

 

Let's take a look at some of the static methods provided here. First, the min method can be passed any Collection and a Comparator: it computes the minimum value in the collection according to that comparator. Its actual code is shown below. 

  public static Object min(Collection coll, Comparator comp)
  {
    if (comp==null)
      min(coll);    //This overloaded method is discussed below

    Iterator i = coll.iterator();
    Object candidate = i.next();
    while(i.hasNext()) {
      Object next = i.next();
      if (comp.compare(next, candidate) < 0)
        candidate = next;
    }

    return candidate;
  }
It iterates over the collection, looking at every value once (so it is in the O(N) complexity class), remembering the smallest value that it examines. It could be argued that the following code should be added before the declaration of Iterator i: 
  if (coll.size() == 0)
    return null;
 That is, if there are no values in the collection, return null (a reference to no value). Instead, the code as written would throw a NoSuchElementException (when next is called to initialize candidate), which certainly is reasonable (there is no element that is the smallest, because there are no elements at all)! Along with min is a matching declaration for max and another for binarySearch that all take some kind of collection (a List in the case of binarySearch) and a Comparator.

The binarySearch method is passed a List, an Object to search for, and a Comparator; it assumes that the list is sorted in increasing order according to the comparator and performs a binary search on it. Actually, the method it uses to compute the answer depends on whether the concrete class implementing List also implements the RandomAccess interface, which itself defines NO methods.

Such an interface is called a tagging interface; its sole purpose is for some classes to say whether it implements the interface (which any class can do, because a tagging interface defines no methods). The Prey subclass in Program #6 should have been a tagging interface; both Ball and Floater should have declared that they implemented this interface so that black holes could ask about objects, instanceof Prey.

A list collection implementing this interface is declaring that the time to perform get and set methods on its list is O(1). In the standard Java collection classes, ArrayList is such a class, but LinkedList which we will study soon, is not: the higher the index to get/set, the longer it takes to perform the method. The binarySearch method checks whether the list it has been asked to search is an instanceof RandomAccess, if so, it calls a method that does lots of gets; if not it calls a method taht uses a that iterates forward and backward, homing in the value to search for.

There are overloaded versions of min, max, and binarySearch that exclude the Comparator parameter. In fact, one is called above in the min method if the Comparator is null. This method assumes that the objects in the list all have a natural ordering (implement the Comparable interface). This interface is similar to, but different than, Comparator. The Javadoc for the Comparable interface is shown below.

 

If a class implements Comparable then its objects knows how to compare themselves with other objects: this is called the natural ordering for the class. So, for example, String implements Comparable (as do all the wrapper classes): it does so with the standard lexical (dictionary) ordering. Thus, if c were some collection of Strings, we could call just Collections.min(c) which would return the smallest String according to this natural ordering. Of course, when we use this simpler method, this is the only answer can be returned, because this is the only way that Java can compare Strings: with the compareTo method built-in to the String class. Using the other version, with a parameter specifying an object constructed from a class that implents Comparator, allows us much more flexibility on how we compare Strings and determine which one is the smallest.

For this reason, I think the Comparator interface is more important than the Comparable interface, but both are used frequently in Java. If there is one dominant/natural ordering for objects, then declare that the class implements Comparable and provide a compareTo method that implements that ordering. You might see something like Comparable[] which specifies an array of objects that all come from classes that implement Comparable interface.

Finally, the code inside min, max, and binarySearch casts the object doing the comparing from Object to Comparable; if that cast fails -the object comes from a class that doesn't implement that interface- then the method throws a ClassCastException. In fact, the same exception is thrown if the list stores different (incomparable) objects: e.g., Java cannot use compareTo to compare a String object and an Integer object. Here is what the Javadoc method details says about this version of min.

 

Two more interesting methods in this class are reverse and even more so shuffle; both take a list as a single parameter, because the other collection classes have no sequential ordering to reverse or shuffle. The first method just reverses the order; the second method randomizes the order. The second method would be useful to call in updateAll method in simulation.Model, so that the same simulton doesn't always have its udpate method called first. This methods runs in O(N): for lists implementing the randomAccess tagging interface it calls get and set directly; for others list implementations (e.g, LinkedList) this iterates through the list, copying all its elements into an array (runs in O(N)), then shuffles the array using the same O(N) algorithm, and then iterates through the array, putting all its values back into the list (also O(N)); so, the ultimate complexity class is still O(N), but the constant is much bigger.

In fact, the Collections class also has two sort methods: one with a Comparator and one without (trying to use the natural ordering specified by Comparable). So, we can sort lists directly without first converting them to an array and then calling Arrays.sort (which, by the way, is overloaded to omit Comparator and use the natural ordering).

Finally, this class includes two interesting kinds of decorators, dealing with "unmodifiability" and "synchronization" respectively. Let's look at the "unmodifiability" property first. The names of these decorator classes have unmodifiable as a prefix and the name of a collection as a suffix (e.g., unmodifiableSet). The suffixes allow names of all the collection interfaces: Collection, List, Set, SortedSet, Map, and SortedMap. Each produces an object that allows all the same methods to be called: all accessors work, but no mutators do: calling a mutator makes the object immediately throw an UnsupportedOperationException. For example, the nested class underlying an unmodifiable set starts as 

  private static class UnmodifiableSet implements Set {
    private final Set s;

    UnmodifiableSet(Set s)
    {
      if (s==null)
        throw new NullPointerException();
      this.s = s;
    }
    
    ...
It is a nested class but not an inner class because it is static. It continues as follows, with accessors/mutators each calling the same named method on the instance variable s or throwing an UnsupportedOperationException, respectively. 
  public int size()
  {return s.size();}

  public Object remove(Object key)
  {throw new UnsupportedOperationException();}
 Thus, we can use this decorator to return an object that refers in whole to our original set but can be examined only, never changed. Often this approach is faster than making a copy of set (another way to ensure the original isn't changed), especially if the set is big and few methods will be called on it (each method call here immediately does another method call, which takes a bit more time).

Synchronization concerns collections shared by two separate threads (think multitasking). With this decorator, if one thread calls a method on the collection, Java is guaranteed to finish it before the other thread can call a method on it. Such code is called threadsafe. We will briefly examine threads in the next lecture. Multitasking is a big, interesting topic in its own right, but a bit out of the scope of this course. The standard collections are not threadsafe but their methods run more quickly (not in different complexity class, but by a different constant factor).

Hash Tables and Hashing In this section we will briefly discuss hash tables, to better understand how collection classes like HashSet and HashMap work and achieve an O(1) complexity class for many of their operations. This discussion is necessarily truncated, and while it will provide us with a lot of insight about hashing, some of the details I describe here are not an accurate description of the actual hash tables Java uses (the standard Java library defines a Hashtable class): so some deailts are a bit simplified, but are the same in spirit, and many of the details are accurately described. There are entire books (and PhD theses) written about hashing.

Before describing hash tables, we will discuss the process of hashing and the hashCode method, which implements this process; note that a hashCode method is defined in the class Object, like toString, and is inherited -and possibly overridden- by every other class. We will first illustrate this method with the String class and discuss hash tables containing only Strings; later we will generalize what we know to arbitrary classes.

Hashing is the process of computing an int value from an object. We will use this value (suitably modified) as an index into an array when we try to see if a value is stored in a set (or lookup the value associated with a key in a map). Here is a slight simplification of the hashCode method defined in the String class: it refers to an instance variable chars that is actually a filled char[], storing all the characters in the String. 

  public int hashCode()
  {
    int hash = 0;
    for (int i = 0; i < chars.length; i++) {
      hash = 31*hash + chars[i];   //promotion of char -> int
    return hash;
  }
For every character, starting at the front, it multiplies the previous hash value by 31, then adds in the ASCII value of the character. For example, "a".hashCode() returns 97 (just its ASCII value); "aa".hashCode() returns 3104 (31*97 + 97). Generally, if String.length() is n (the chars array contains n values), then its hashed value is given by the formula 
 chars[0]*31n-1+chars[1]*31n-2+ ... +chars[n-2]*311+chars[n-1]
 So, "15-200".hashCode() returns 1,453,165,193, and "Richard Pattis".hashCode() returns -125,886,044! Yes, because of arithmetic overflow and the standard properties of binary numbers, the result might be negative. Recall that Java does not throw any exceptions when arithmetic operators produce values outside of the range of int: hashing is one of the few places where this behavior produces results that are still useful.

Now, let's transition to discuss hash tables themselves. The simplest model of the underlying data structure in a hash table is List[]: an array, where each index stores a list of values that have all hashed to that same spot. We will assume we are using the concrete class, e.g. ArrayList, for this discussion. For purposes of illustration, lets use an array of length 10. We will simplify our typical pictures of arrays and list objects to the bare minimum, as shown below.

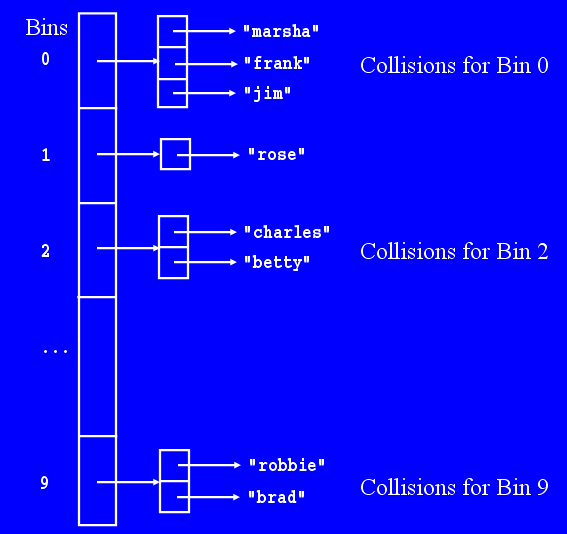
  We call each index in the hash table a bin. We would declare and initialize this hash table as follows: 
  List[] ht = new ArrayList[10];
  for (int i=0; i<ht.length; i++)
    ht[i] = new ArrayList();
 Now, let's put everything together and discuss how to use a hashCode value with a hash table to perform a useful operations on sets. First, let's see how to add an object to a set by using its hash table. 
  boolean add(Object o)
  {
    int i = Math.abs(o.hashCode()) % ht.length;
    if (ht[i].contains(o))
      return false;
    
    ht[i].add(o);
    return true;
  }
 First, we compute o.hashCode(), taking its absolute value, and finally computing its remainder modulo the hash table's length: the end result is a number that we can use as an index in the hash table (i.e., a value between 0 and ht.length-1). We then check whether this object is already in the list (a linear search) and if so, return false immediatley (no duplicates are put in the set); otherwise, we add the value to the list (at the end) and return true.

For example, "marsha".hasCode() returns -1081298290, which for this hash table results in an index of 0. Thus, "marsha" belongs in bin 0; if the table were originally empty (every ArrayList was empty), then "marsha" would be placed, as shown, first in the list referred to by bin 0.

In reality the index is computed by the expression (o.hashCode() & 0x7FFFFFFF) % ht.length which uses a hexidecimal number and the logical and operator to mask off the sign bit of the binary number making it non-negative; don't worry about this detail, which is faster than computing the absolute value.

Likewise, we can write equally simple methods to check for containment and removal of values from the set, with most of the "post hashing" work being done by the standard list methods. 

  boolean contains(Object o)
  {
    int i = Math.abs(o.hashCode()) % ht.length;
    return ht[i].contains(o);
  }

  boolean remove(Object o)
  {
    int i = Math.abs(o.hashCode()) % ht.length;
    return ht[i].remove(o);
  }

Now we will see why toString methods for classes implemented by hash tables produce their output in a weird order. The easiest way to write the toString method is just to iterate over all the bins, first to last, and in each bin iterate over its list of values, accumulating in a String everything to return. The real toString method uses a StringBuffer, which catenates more efficiently than String (we will discuss this class at the end of the semester). 

  String toString(Object o)
  {
    boolean first = true;
    String  answer = "[";

    for (int i=0; i<ht.length; i++)
      for (int h=0; h<ht[i].size(); h++) {
        answer += (first ? "" : ",")+ht[i].get(h);
        first = false;
      }

    return answer+"]";
  }
This was all very simple (well compared to anonymous inner-classes everything is simple), but how can it be efficient? That discussion is the most interesting part of learning about hash tables. If you're like me, you'll feel a bit cheated, but you'll get over it.

First, we are going to assume a "good" hash function. That is, given all the possible values that we will put in the hash table, they are equally spread out in the bins (about the same number would end up in each bin).

Aside: When two objects hash to the same bin it is called a collision. Theoretically, a perfect hash function computed with a hash table of length N should be able to compute different values (no collisions) for N elements; but such hash functions are difficult to find and can be very expensive (in computer time) to run. So,we will assume collision can occur, which is why we use lists in each bin: to store all the colliding objects.
This means that if we stored N values in a hash table with M bins, then the complexity class of adding, checking, or removing a value would be O(N/M), because after we hash the object to compute its bin, we expect about N/M values to be in each bin, and we are using list operations (contains and remove) that do linear searches of these lists. If M is a constant the complexity class O(N/M) should be the same O(N)! Now comes the magic.

What if we knew how big N would be, so we made M exactly that big: M=N. Then the complexity class of adding, checking, and removing would be O(N/N) = O(1)! In fact, if M were any fixed percentage of N (say N/k), then the complexity class of these operations would be O(N/(N/k)) = O(k) = O(1). That is, if M were half N, the complexity class would be O(N/(N/2)) = O(2) = O(1) but the constants would make such a hash table take twice as long as the bigger hash table; if M were N/10, the complexity class would be O(N/(N/10)) = O(10) = O(1) but the constants would make such a hash table take ten times as long as the bigger hash table.

So, the bigger M (the number of bins) the fewer values are in each bin, and the faster the list methods run. Of course, there is a limit: there is no reason to make the hash table have more than N bins, because that just means lots of bins will be empty. We will never lookup information in these empty bins (once all N values have been added) so they just occupy extra space but do not improve performance.

The assumption that we know N is a bad one, and we do not really make N bins in the hash table when it is constructed. We discard this assumption, just as we did for arrays, by allowing hash tables to double their size whenever they start to fill up. Size-doubling for hash tables requires that we create a new hash table (with twice as many bins), then iterate over every value in the old hash table, adding it in the new hash table by rehasing it. Notice that there is NO GUARANTEE that an object that hashed to some index in the old table will hash to the same index in the new table: when taking % ht.length with a different length, the remainder is likely to be different too! Here is the code that implements doubleLength for a hash table. It uses the same iteration scheme (first over bins, then over the elements in each list) as toString. 

  void doubleLength()
  {
    List[] oldHt = ht;
    ht = new ArrayList[ht.length*2];
    for (int i=0; i<ht.length; i++)
      ht[i] = new ArrayList();

    for (int i=0; i<oldHt.length; i++)
      for (int h=0; h<oldHt[i].size(); h++)
        add(oldHt[i].get(h));
  }
Note that we create 2N new ArrayLists and iterate over the N values in the old hash table, adding each to the new hash table (add is an O(1) operation), so just as in array doubling, the complexity class of doubling the length of a hash table is O(N).

So, when does Java double the length of a hash table? It depends on the load factor, which is either specified in the constructor of some class that uses a hash table, or has a default value (typically of .75) The load factor of a hash table is the ratio N/M; it gets bigger as more values are added to a hash table. When it exceeds the specified limit, the hash table's length is doubled (actually, probably by a factor of 1.5, which is what collections like list do). So, in the default case, if a hash table exceeded being 75% full (by adding the 76 value in a hash table with 100 bins), it will increase its length. As with array length doubling, we don't want to do it too often, so when we double we make the array much bigger, making the load factor much smaller. This is a classic time vs. space tradeoff: by using more space (bins in a hash table) we can reduce the time it takes to execute various methods.

Throughout this discussion, we have ignored the time it takes Java to compute the hashCode of an object. Obviously this method should run relatively quickly compared to the overhead needed to start and complete a hash table search. There is often a tradeoff between how quickly the hashCode method runs and how uniformly it computes bin values (which, by the way, does not depend solely on the hashCode method itself, but also on the number of bins in the hash table). In any case, the time it takes to execute the hashCode method is independent of N, the number of items in the hash table.

hashCode methods If we write our own class that will be used in some collection backed by a hash table (a set, or the key in a map), we should override the inherited hashCode method. The method we write should be quick and should produce few collisions. The only rule we must follow is that 
x.equals(y) implies x.hashCode() == y.hashCode()
 That is .equals objects must hash to the same bin, regardless of the hash table length; but, also notice the implies goes just one way: if objects produce the same hash code they may or may not be .equals (it might just be a collision).

Typically a hashCode method will call hashCode on all its instance variables and numerically combine them into a single value. For example, the AbstractList class defines the following hashCode method relying on the iterator to examine each value it stores (and to find its hashCode and add them up in a weighted sum). 

  public int hashCode()
  {
    int hashCode = 1;
    Iterator i = iterator();
    while (i.hasNext()) {
      Object obj = i.next();
      hashCode = 31*hashCode + (obj==null ? 0 : obj.hashCode());
    }

    return hashCode;
  }
If a class just inherits hashCode and does not override it, it will not be using all its intersting instance variables to compute its hash value. There might be very many collisions, slowing down the methods of the the collection class using it.
Mutation and Caching The final two topics on hashing are related
  • Why we should not mutate an object that is in a collection that employs hashing.
  • Why we can cache hash values for immutable objects.
We have seen that hash tables store an object in some bin; which one depends on the value returned when the hashCode method was called on the object when it was added to the hash table. We have also seen that the hashCode method typically returns a result that depends on the state of the object (the hash codes of its instance variable). If we share an object with a hash table and then mutate it, the object is likely to be stored in the wrong bin in the hash table (according to what value its hashCode now returns), so searching for it, removing it, etc. will probably not work correctly. Thus, the note in the Javadoc for both HashSet and HashMap. But, while mutating the key in a map is forbidden, there is no problem mutating the value, because hashing is done on the key only, not its associated value.

Given this prohibition, using an immutable class in a hash table is a perfect match, since it contains no mutators. String and all the collection classes are immutable. In fact, the String class uses caching (remembering a computed value) for hashing -kind of rolls off the tongue: caching for hashing. Caching is another classic time vs. space tradeoff: we store a computed value if we expect that we might have to compute it again; the second time we just return the precomputed value.

We can now show a more accurate version of the hashCode method defined in the String class. Assume that hashCode is an instance variable declared in this class. 

  public int hashCode()
  {
    if (hashCode != 0)
      return hashCode;

    int hash = 0;
    for (int i = 0; i < chars.length; i++) {
      hash = 31*hash + chars[i];   //promotion of char -> int
    return hashCode = hash;
  }
So, the first time the hashCode method is called, it computes its value and before returning it, stores it in the hashCode instance variable. The next time it is called, it just immediately returns this value. Because the String class is immutable, the value hashCode returns should always be the same!

In fact, for mutable classes we can extend the "modification count" trick that we used for iterators and combine it with caching. When we call the hashCode method for the first time on an object, we store its hash code AND the modification count of the object. For a subsequent call to the hashCode method, if the current modification count is the same, we can just return the cached hash code; if it is different, we must recompute the hash code and re-store it and the new modification count.

Reading Java Classes The source code for all of the classes in the standard Java library is stored in a .zip file format (current about 10Mb; probably 2-5 times that size when unzipped).

In Java 1.3, this file is typically stored in the top level folder for Java (e.g., jdk1.3.1_04) in the file named src.jar; in Java 1.4, this file is typically stored in the top level folder for Java (e.g., j2sdk1.4.1_01) in the file named src.zip In the newer versions, not only is the file in a zip format, its extension is also zip. On a Windows PC, you can drag either of these files into the zip icon, and in the case of scr.zip you can just double-click it. The result is that you can double-click on a file in the zip window and load it into a Metrowreks editor to view it, or you can copy the file out of the zip window onto, say the desktop, and examine/edit it there.

As mentioned in lecture, these classes are documented with Javadoc and written fairly simply: even beginners might be able to understand the code, or at least parts of the code, that they contaisn. Although not as useful as the Javadoc html pages documenting these classes, the code for these classes is a great resource for understanding the Java way of doing things, such as how hash tables are really used to implement collection classes (there are a lot more details than we got into here). Another interesting method to examine is the sort method in the Arrays class.

Generics in Java 1.5 Out of time: see Java Generics a pdf tutorial.
Problem Set To ensure that you understand all the material in this lecture, please solve the the announced problems after you read the lecture.

If you get stumped on any problem, go back and read the relevant part of the lecture. If you still have questions, please get help from the Instructor, a TA, or any other student.

The programming assignment will throroughly test your ability to use all the collecton classes.

  1. The binarySearch method assumes, as a precondition, that the list it is passed is sorted according to the comparator it is passed. Explain why it isn't a good idea for this method to check this preconditon, which it could easily do by applying the comparator between each adjacent pair of values in the list?

  2. Explain how the hashCode method for the Integer wrapper class computes its value.