| Introduction |
In this lecture we will continue our study of trees by examining a few special
kinds of trees.
First we will discuss heaps, which are trees with a special order and structure
property: these trees are perfectly suited for implementing a fast priority
queue collection class (and an O(NLog2N) sorting method).
Second we will discuss how to represent and process N-ary trees, where each
parent can store any number of children; we can use N-ary trees in
applications like file directories.
Third, we will discuss how to represent arithmetic expressions in structure
trees, including how to create (with a stack) and evaluate such expression
trees using the rules of parentheses and operator precendence.
This is like writing a tiny parser for expressions, and is covered in any
course on compiler writing.
Finally, time permitting, we will discuss digital trees, which are a special
type of N-ary tree in which searches can be performed exceptionally fast
O(1), because the time is based on the size of the value stored, not the
number of values stored.
The primary goal of this lecture is to understand these special trees via pictures and algorithms (which modify pictures). We will examine some methods, actually implemented in Java, but that is not the focus of this lecture: the concepts are more important than the code. |
| Heaps |
A heap is a binary tree with a special ordering property and a special
structure property.
Taken together these two properties allow for a very efficient implementation
of priority queues (measured both in time and space).
Here we will discuss min-heaps: priority queues use max-heaps.
|
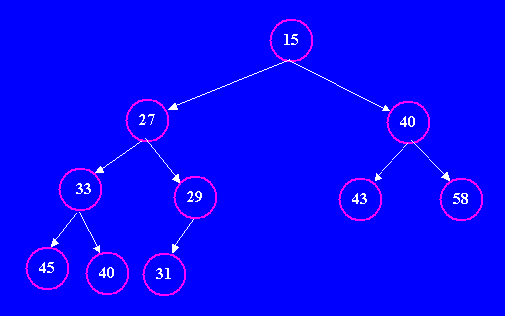
|
The first observation to make about heaps is that they are useless for doing binary searches. This ordering property doesn't help us: if searching for a value, we do not know whether to look in the left or right subtree, because the ordering property dictates only that larger values are in the subtrees. But the ordering/structure property for heaps makes it very easy (quick) to add a new value and remove the smallest value. We will discuss the operation of these two algorithms next. The following algorithm inserts a new value into a heap, ensuring that both the ordering and structure properties are invariant: if true before the insertion, they are true after the insertion. To insert a new value in a heap:
|

|
Notice that both the ordering property and the structure property remain satisfied after performing the insertion (with the new value, 18, percolating almost to the root of the tree, but not quite). In fact, if we had inserted 10, it would have percolated upwards all the way to the root of the tree (because it would be the smallest value in the entire heap). To build a heap with N values, we would perform this insertion operation N times, starting with an empty tree. Practice inserting a few more values until you get the general idea of the algorithm Note that the complexity class of inserting a value is truly O(Log2N), because by the structure property, heaps always store prefectly balanced trees (their height is always the log of their size). And, the number of percolations performed is at most the height of the tree. Next, we will examine an algorithm for removing the minimum value from a Min-Heap, ensuring that both the ordering and structure properties are invariant: if true before the removal, they are true after the removal. To remove the minimum values in a heap:
|
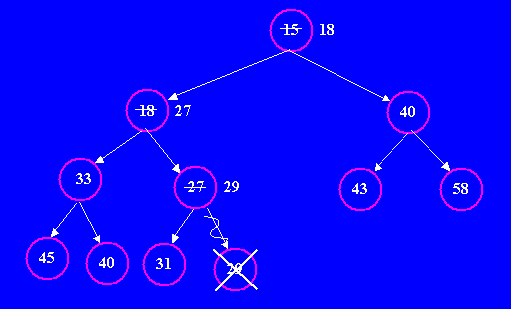
|
See the nodes where the values 18, 27 and 29 have ultimately moved. Notice that both the ordering property and the structure property remain satisfied after performing the removal. Practice removing a few more values until you get the general idea of the algorithm Note that the complexity class of removing the minimum value is truly O(Log2N), because by the structure property, heaps always store prefectly balanced trees (their height is always the log of their size). And, the number of percolations performed is at most the height of the tree. This means that the complexity class of enqueuing N values and then dequeuing N values (the standard way to measure the complexity class of a collection class) is O(N Log2N) + O(N Log2N) = O(N Log2N). This complexity class is much better than our previous implementations, which were O(N2) (when either enqueue or dequeue was O(1) while the other was O(N). Having each operation O(Log2N) (worse than O(1) but better than O(N) seems to balance things out better. The logarithm function is closer than constant than to linear growth. In fact, we can sort an array in O(N Log2N) by the equivalent of enqueuing all its values and then dequeuing them. Finally, the structure property of heaps allows us to easily store them as contiguous values in arrays, without the use of explicit child/parent references: references to left/right children and parents can be calculated via the indexes. To do this, we do the following:
|
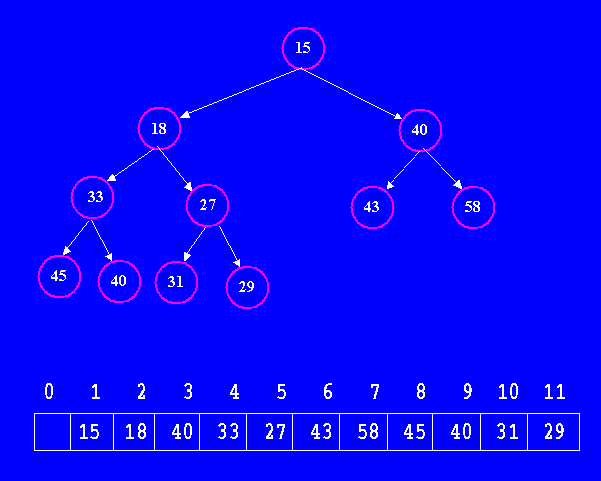
|
Note that the parent of any child stored in index i is stored at index i/2. The left child of the root is stored at index 2 (its left and right children are stored at indices 4 and 5 respectively); the right child of the root is stored at index 3 (its left and right children are stored at indices 6 and 7 respectively). By continuing this process, we can observe that every index is filled in and there are no collisions (multiple values stored in the same index). Thus, we can unambiguously store any heap of N values in an array of size N+1, storing its nodes uniquely between indexes 1 and N. As the algorithms above require, we can easily find the location of the node to add (for insertion) or node to remove (deletion): index N+1 and index N respectively. |
| General N-ary Trees |
Binary trees store references to their left and right subtrees: each parent
has exactly 0, 1, or 2 children.
We will now explore a few interesting ways to generalize trees to allow each
parent to store references to any number of children.
Such trees are called N-ary trees, and we can use them to represent the
tree structure of a file system, where every node is either a file, or a
folder (that can include other files and folders).
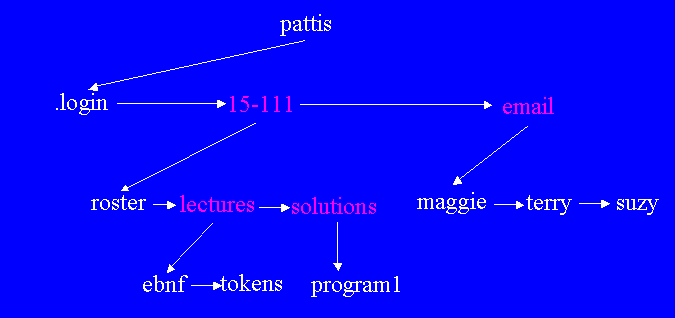
Here is an example of an N-ary tree representing a directory tree (with folder names in pink and file names in white)
|
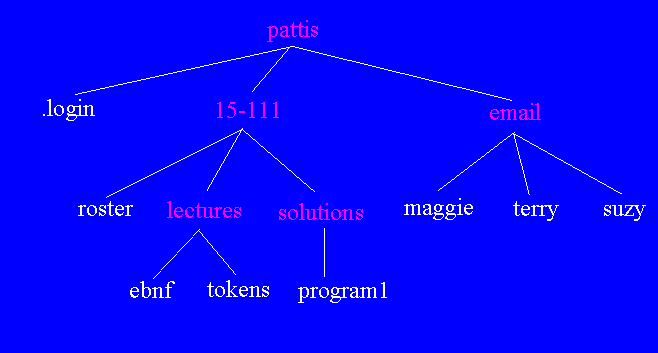
There are many ways to implement an N-ary tree structure.
We could, for example, have one instance named children that stored
a reference to a collection class of children: List if there was an
important order among its children, and Set if there was no important
order; of course, we can use an array for this information too, but using a
collection class often makes things simpler.
public class FolderFile {
public FolderFile (String s)
{name = s; children = new HashSet();}
public String name;
public Set children;
}
Given this representation, here is a recursive method that prints the names of
all the the folders and files stored inside the FolderFile supplied to
its parameter (no matter how many levels deep).
It uses a combination of iteration and recursion to reach every node in the
tree.
public static void printNames (FolderFile ff)
{
System.out.println(ff.name);
for (Iterator i = ff.children.iterator(); i.hasNext(); ) {
FolderFile aChild = (FolderFile)i.next()
printNames( aChild );
}
}
Note that this is a form of preorder traversal: a node is printed before the
recursive call made on its children.
The program Directory Lister shows how we can explore directory structures in Java, using the File class from Java's standard library. In fact, Java uses arrays to list all the files available in a folder, so they are processed in a manner similar to the code above. Surprisingly, we can also use a standard binary tree to store an N-ary tree, when we assign the two references different meanings. The basic idea behind N-ary trees stored as binary trees is that that each node refers to its first child and its next sibling. Thus, as with regular binary trees, we still define such trees using two recursive references; but their meanings, and how such trees are processed are very different. The general form for defining N-ary tree nodes is public class NTN {
public int value;
public NTN firstChild,sibling;
public NTN (int i, TN fc, TN s)
{value = i; firstChild = f; sibling = s}
}
For example, to represent the directory tree above, we use NTNs
with the following references.
Notice that each node refers downward (and to the left) for its first child,
and rightward to its next sybling.
|
|
For actually defining directory data, we will define the following three classes in a small inheritance hierarchy. DirectoryEntry is the superclass for both File and Folder. It supplies code for a variety of methods, including getFirstChild (which always returns null but is overridden by Directory) and getSize (which always returns 0 but is overridden by File). All directory entries have siblings, but only Folders have children. public class DirectoryEntry {
public DirectoryEntry (String name)
{this.name = name; next = null;}
public DirectoryEntry getFirstChild()
{return null;}
public DirectoryEntry getNextSibling()
{return next;}
public void addSibling(DirectoryEntry de)
{
DirectoryEntry c = this;
for (; c.next != null; c=c.next)
{}
c.next = de;
}
public int getSize()
{return 0;}
private String name;
private DirectoryEntry next;
}
public class File extends DirectoryEntry {
public File (String name, int size)
{super(name); this.size = size;}
public int getSize()
{return size;}
private int size;
}
public class Folder extend DirectoryEntry {
public Folder (String name)
{super(name); firstChild = null;}
public DirectoryEntry getFirstChild()
{return firstChild;}
public void addChild(DirectoryEntry de)
{
if (firstChild == null)
firstChild = de;
else
firstChild.addSibling(de);
}
private DirectoryEntry firstChild;
}
Now suppose that we wanted to compute the height of this N-ary tree
(how deep one has to go to get to the deepest folder or file).
We could use the following code, which combines iteration (for siblings)
with recursion (for children).
public static int height (DirectoryEntry de)
{
if (de == null)
return -1;
else {
int maxChildHeight = -1;
for (DirectoryEntry c=de.getFirstChild(); c!=null; c=c.getSibling()) {
int childHeight = height(c);
if (childHeight > maxChildHeight)
maxChildHeight = childHeight;
}
return 1 + maxChildHeight;
}
}
We can write this code amazingly more elegantly and compactly by using double
recursion.
It does require two methods.
First,
public static int height (DirectoryEntry de)
{return 1 + heightHelper(de.firstChild);}
where heightHelper computes the maximum height of a node
or any of its subsequent siblings.
public static int heightHelper (DirectoryEntry de)
{
if (de == null)
return -1;
else
return Math.max( 1+heightHelper(de.firstChild),
heightHelper(de.getSibling) );
}
Finally, if we wanted to compute the total size of all the files in a directory
(like adding up the sizes in all the nodes in a binary tree), we could use
the following code (also, two methods)
public static int size (DirectoryEntry de)
{
if (de == null)
return 0;
else
return de.getSize() + sizeHelper(de.firstChild);
}
where sizeHelper computes the size of a node
or any of its subsequent siblings.
public static int size (DirectoryEntry de)
{
if (de == null)
return 0;
else
return de.getSize() + sizeHelper(de.firstChild) + sizeHelper(de.getSibling);
}
|
| Expression Trees |
We can also use binary trees to model Java expressions (using binary and unary
operators -whose left subtrees are empty and whose right subtrees contain
the expression to apply the unary operator to).
In such trees, operators are all internal nodes and literals are all leaf
nodes.
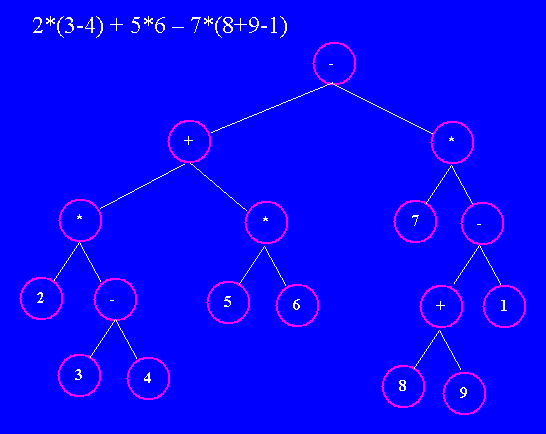
The following picture illustrate an arithmetic expression written in infix
form, and its expression tree.
|
|
It it interesting to observe that the Reverse Polish Notation (RPN) translation of any expression can be computed by a postorder traversal of its tree (printing the value, operator or constant, of each node). Note that there are no parentheses in the tree; the operator precedence (including parentheses which override precedence) can alter the structure of the tree, even though they don't appear in the tree proper. Also note that by modeling an expression as a tree, we can answer certain questions about the expression by computing information on the model. For a computer with a single arithmetic unit, the amount of time it will take to evaluate an expression is computed by the number of internal nodes. For a computer with many arithmetic units, the amount of time it will take to evaluate an expression is computed by the height of the tree (because all operators at the same depth bacn be computed at the same time by the multiple arithmetic units). We can use inheritance to model expressions easily. The classes definining expression trees (both abstract and concrete) form the following inheritance hierarchy. |
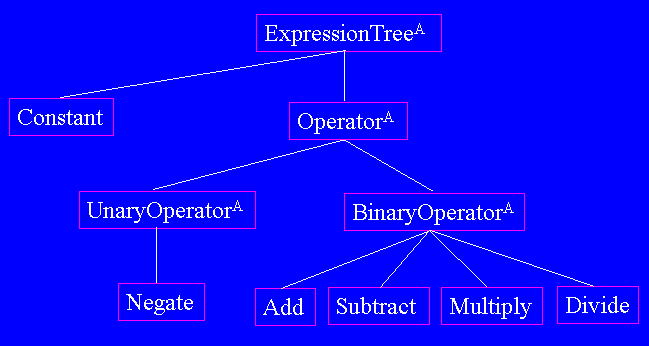
At the top of this hierarchy (descended from Object) is
generic class ExpressionTree, which is defined as follows.
public abstract class ExpressionTree {
public abstract int evaluate();
public abstract String postfix();
//This is called a "Factory" Method. It constructs an expression tree
public static ExpressionTree makeET
(String op, ExpressionTree left, ExpressionTree right)
{
if (op.equals("+"))
return new Add(left,right);
else if (op.equals("-"))
return new Subtract(left,right);
else if (op.equals("*"))
return new Multiply(left,right);
else if (op.equals("/"))
return new Divide(left,right);
else if (op.equals("^"))
return new Power(left,right);
else if (op.equals("~"))
return new Negate(right);
else
throw new IllegalArgumentException
("ExpressionTree.makeET: illegal operators = " + op);
}
}
So the main methods, which are abstract, compute the value of an expression
and produce the postfix (RPN) String representation of an expression.
We can write the Constant class as a direct, conctete subclass of this
one, trivially implementing the postfix and evaluate methods.
public class Constant extends ExpressionTree {
public Constant (int value)
{this.value = value;}
public int evaluate()
{return value;}
public String postfix()
{return ""+value+" ";}
private int value;
}
We add another layer of abstraction when defining the simple Operator
subclass (extending ExpressionTree).
public abstract class Operator extends ExpressionTree {
public abstract String getOpSymbol();
}
And add a final abstract layer by defining the BinaryOperator class
(the UnaryOperator class is defined similarly).
Notice that the abstract postfix method is made concrete at this level
of the hierarchy (the getOpSymbol method is still abstract and will
be specified in a subclass).
It uses a postorder traversal to compute the postfix form of the left and
right subexpressions, followed by the current operator.
public abstract class BinaryOperator extends Operator {
public BinaryOperator (ExpressionTree left, ExpressionTree right)
{
this.left = left;
this.right = right;
}
public ExpressionTree getLeft()
{return left;}
public ExpressionTree getRight()
{return right;}
public String postfix()
{return left.postfix() + right.postfix() + getOpSymbol() + " ";}
private ExpressionTree left,right;
}
Finally, with this infrastructure, it is very easy to specify a new class
that represents an operator, such as Multiply specified below.
public class Multiply extends BinaryOperator {
public Multiply (ExpressionTree left, ExpressionTree right)
{super(left,right);}
public int evaluate()
{return getLeft().evaluate() * getRight().evaluate();}
public String getOpSymbol()
{return "*";}
}
Notice that evaluation uses a postfix traversal of the tree: it recursively
evaluates the left and right subtrees (their classes determines how they
evaluate their values), and then performs the arithmetic operation specified
by this node).
Download Expression Trees for the entire specification of these classes, and a driver program that uses a StringTokenizer and Stack to translate infix expressions (using operator precedence and parentheses) into expression trees, and then print their postfix form and evaluate the expression tree. Could augment this program by using a Map to store associations between variables and values, so that we could add a Variable class to the heirarchy above. Then, we could add the = operator, and evaluate expressios in the context of the variable map; at this point we have built an interpreter for a simple calculator. |
| Digital Trees (aka Tries) |
I will discuss these in class. |
| Problem Set |
To ensure that you understand all the material in this lecture, please solve
the the announced problems after you read the lecture.
If you get stumped on any problem, go back and read the relevant part of the lecture. If you still have questions, please get help from the Instructor, a TA, or any other student.
|