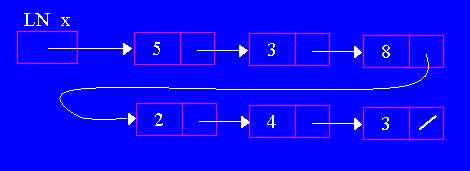
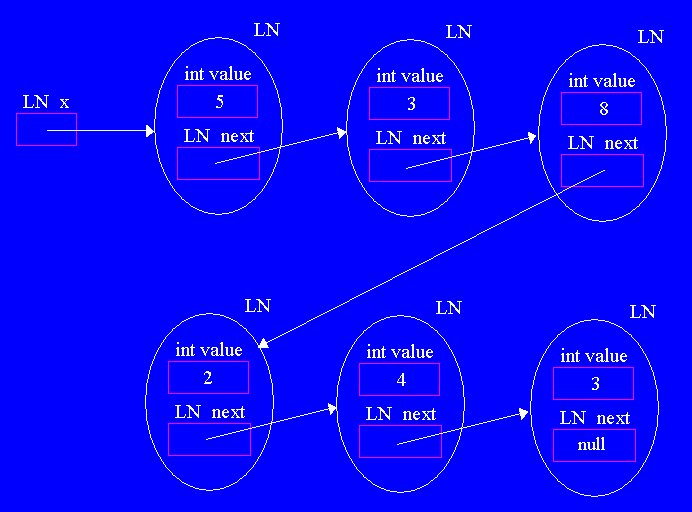
| Building Linked Lists |
It is easy to update the variable x from null (refering to an
empty list) to refer to a list with one value, say 5:
x = new LN(5,null);
Likewise, we can extend this list to a second value, say 2 by writing
x.next = new LN(2,null);
And, we can extend this list to a third value, say 7 by writing
x.next.next = new LN(7,null);
We can continue in this manner to build a linked list manually.
In fact, we can even write this as one complicated assignment:
x = new LN (5, new LN (2, new LN(7, null)));
But, this method requires us to write code manually for every linked list that
we must build.
Now let us examine ways to build lists automatically, say by reading values
from a file.
The following simple code reads all the values from a file (assume
TypedBufferReader tbr has been declared and intialized) and places
them in a linked list.
for (;;)
try {
x = new LN(tbr.readInt(), x);
}catch (EOFException eofe) {break;}
Note the x on both size of the equal sign.
Generally, the code x = new LN (someValue, x); adds someValue at
the front of the list (whether the list is originally empty or not: try both
ways) making its next refer to the original linked list.
Note that executing the statement x = new LN(tbr.readInt(),x); is in
the complexity class O(1): no matter how big of a list x refers to,
this operation is completed in constant time (independent of the list size).
Thus, since this operation is executed N times, the complexity class of reading
in a list is O(N).
The only drawback of this code is that the values appear in the linked list in
the reverse of the order in which they appear in the file (which may or may
not be a problem depending on how we want to process the data); hand simulate
this code for reading a file with just a few values in it to verify this
statement.
If we need the sequence of values stored in the same order as they appeared in
the file, we have many possible ways to accomplish this task.
First, we can reverse the list (see the next lecture), or make the code more
complicated.
Below, let's examine the code needed to place a new list node at the rear of a
linked list.
The strategy for doing so can be easily described:
- If the list is empty, change x to refer to the new list node
- If the list is not empty, locate its last list node (the only one
currently storing null in its next instance variable), then
store a reference to the new list node in that next field.
In both cases, the new list node stores null in its next
instance variable, because it is becoming the "new" last node in the list.
Assume that int someValue stores the value we want to add at the end of
the list.
We can translate this description into the following Java code.
if (x == null)
x = new LN (someValue,null);
else {
LN r = x;
for (; r.next!=null; r=r.next)
{}
r.next = new LN(someValue,null);
}
There are a few interesting aspects of this code.
- The cursor r must be declared outside the for loop, not
inside it.
The reason is that r (which is made to refer to the current last
node in the list) must be altered after the loop terminates; any
variable declared inside the loop would not be usable outside the loop
body.
- The purpose of the loop is to store into r a reference to the
current last node in the list: so all it does is advance r until
it refers to a list node whose next stores null.
So note that the body of the loop is just {}: this empty block
statement could be replaced by just the empty statement ; but
we prefer to emphasize this "lack of actions" with an empty block.
Some programmers would even write {\*nothing*\} as the body of the
loop.
- The continuation test is only r.next!=null; the first time we check
this test we know that r stores a non-null reference (see the
if statement).
Likewise, for each subsequent loop we know that r, when updated to
r.next will also store a non-null value.
Thus, this code will never throw a NullPointerException.
An alternative way to write this code (less elegant, in my opinion, but
possibly easier to understand) is
if (x == null)
x = new LN (someValue,null);
else {
for (LN r=x ;; r=r.next) //Continuation test is always true
if (r.next == null) {
r.next = new LN(someValue,null);
break;
}
}
Given this code for adding a new value at the end of a linked list, we can now
write code that reads all the values from a file and places them in a linked
list in the correct order, using two nested loops.
for (;;)
try {
int someValue = tbr.readInt();
if (x == null)
x = new LN (someValue,null);
else {
LN r = x;
for (; r.next!=null; r=r.next)
{}
r.next = new LN(someValue,null);
}
}catch (EOFException eofe) {break;}
Although this code is correct, it can be very inefficient: its complexity
class, if N is the number of values read, is O(N2).
The source of the inefficiency is repeatedly scanning the linked list to find
its end.
The first time requires scanning past 0 nodes; the second time requires
scanning past 1 node, the third time requires scanning past 2 nodes, ... the
Nth time requires scanning past N-1 nodes.
So, to insert N nodes into this list requires scanning 0+1+2+...+N-1 nodes.
We have seen this before (and should memorize if we haven't already): the
general formula for 1+2+...+N is N(N+1)/2, so in this case the result is
(N-1)(N-1+1)/2 = N(N-1)/2.
Of course, this is in the complexity class O(N2).
For inserting 1,000 nodes in a list requires scanning 499,500 nodes;
for inserting 1,000,000 nodes in a list requires scanning about
500,000,000,000 nodes!
Even at 1 billon scans per second, that would take 8 minutes.
Everett Dirkson, an ancient Senator from Illinois, was once quoted as
"A billion dollars here, a billion dollars there, pretty soon it adds
up to real money".
A later day Dirkson, one in computer science, might say the same about
nanoseconds adding up to real time.
We can drastically speed-up this process (changing its complexity class back
to O(N)) by "caching" a reference to the last node in a list (and updating
it whenever a new node is added at the end).
In this way we can eliminate scanning altogether (or another way to look at it
is scanning each newly added list node once, and remembering it: this is
similar to amortized complexity computations).
The technique of caching is a wonderful example of a space for time tradeoff:
by increasing the amount of space (by storing an extra reference) we can
decrease the amount of running time.
The code to accomplish this same task more efficiently (in time; a bit less in
space) is
LN lastCache = null;
for (;;)
try {
int someValue = tbr.readInt();
if (lastCache == null)
lastCache = x = new LN (someValue,null);
else {
lastCache.next = new LN(someValue,null);
lastCache = lastCache.next;
}
}catch (EOFException eofe) {break;}
In fact, as an extra bonus this code is even simpler (less confusing) than the
code shown above, if we understand how the lastCache is initialized
and used.
Java masochists could "simplify" the else block by writing the single
statement (similarly to what appears before the else)
lastCache = lastCache.next = new LN(someValue,null);
whose double assignment does the job of both statements in the block.
Notice that
lastCache.next = lastCache = new LN(someValue,null);
with the order of the two values receiving the assignment, FAILS TO DO THE
JOB.
|