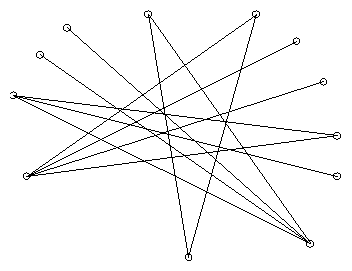
The rotating caliper graph (shown above) has as its edges the tangent pairs considered by the rotating caliper algorithm. Equivalently an edge xy is in the rotating caliper graph exactly when all input points lie between the two parallel lines through x and y and perpendicular to xy. This definition applies to arbitrary point sets, but like the farthest point Delaunay triangulation the rotating caliper graph only connects convex hull vertices.
The rotating caliper graph has some interesting properties. First, in a natural expected-case model of dynamic geometric optimization algorithms, the expected number of RCG edges that change per point insertion or deletion is only a small constant (and these edges can be found quickly using some data structures to keep track of the convex hull). As a consequence, we can maintain the RCG itself, and the width and diameter of the point set, in logarithmic expected time per operation. Second, the RCG is a thrackle. This class of graph drawings, defined by John Conway, consists of graphs in which each pair of edges has a single intersection point (which may either be a vertex or interior to the two edges). Conway asked whether every n-vertex thrackle has at most n edges, and the question still remains open if curved edges are allowed. Straight-line-segment thrackles such as the RCG are quite well understood.
[From "Average Case Analysis of Dynamic Geometric Optimization".]
From the Geometry Junkyard,
computational
and recreational geometry.
David Eppstein,
Theory Group,
ICS,
UC Irvine.
Last update: .