Adventitious geometry.
Quadrilaterals in which the sides and diagonals form
more rational angles with each other than one might expect.
Dave Rusin's known math pages include
another article on the same problem.
BitArt spirolateral
gallery (requires JavaScript to view large images, and Java to view
self-running demo or construct new spirolaterals).
Brahmagupta's formula.
A "Heron-type" formula for the maximum area of a quadrilateral,
Col. Sicherman's fave. He asks if it has higher-dimensional
generalizations.
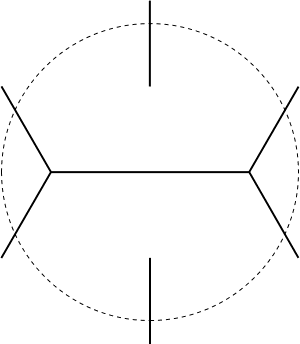
Building a better beam detector.
This is a set that intersects all lines through the unit disk.
The construction below achieves
total length approximately 5.1547, but better bounds were previously known.
The
Cheng-Pleijel point. Given a closed plane curve and a height H,
this point is the apex of the minimum surface area cone of height H over
the curve. Ben Cheng demonstrates this concept with the help of a Java applet.
Curvature of crossing convex curves.
Oded Schramm considers two smooth convex planar curves crossing at at
least three points, and claims that the minimum curvature of one is at
most the maximum curvature of the other. Apparently this is related
to conformal mapping. He asks for prior appearances of this problem
in the literature.
Fourier
series of a gastropod. L. Zucca uses Fourier analysis to square
the circle and to make an odd spiral-like shape.
Fractal fiber bundles.
Troy Christensen ponders origami on the fabric folds of spacetime.
Gallery of interactive on-line geometry.
The Geometry Center's collection includes programs for generating
Penrose tilings, making periodic drawings a la Escher in the Euclidean
and hyperbolic planes, playing pinball in negatively curved spaces,
viewing 3d objects, exploring the space of angle geometries, and
visualizing Riemann surfaces.
Geek bodyart.
Geometric calculations for fitting your piercings.
Geometry of alphabets.
Sacred geometry wackiness from the Library of Halexandria.
Something about how the first verse of Genesis forms a dodecahedron, or
a flower, or maybe a candlestick, somehow leading to squared circles,
spiraling shofars, and circumscribed tetrahedra.
Geometry
problems involving circles and triangles, with proofs.
Antonio Gutierrez.
Gömböc, a
convex body in 3d with a single stable and a single unstable point of
equilibrium. Placed on a flat surface, it always rights itself; it may
not be a coincidence that some tortoise shells are similarly shaped.
See also Wikipedia, Metafilter, New
York Times.
Ham
Sandwich Theorem: you can always cut your ham and two slices of
bread each in half with one slice, even before putting them together
into a sandwich.
From Eric Weisstein's treasure trove of mathematics.
Helical geometry.
Ok, renaming a hyperbolic paraboloid a "helical right triangle"
and saying that it's "a revolutionary foundation for new knowledge"
seems a little cranky but there are some interesting pictures of shapes
formed by compounds of these saddles.
Imagine, Geometry.
Starting with visions of pre-natal consciousness in 1968.
Primary-colored animations of platonic solids
turn your brain cells into puffed, expanded dodecahedra.
Jordan sorting. This is the problem of
sorting (by x-coordinate) the intersections of a line with a simple
polygon. Complicated linear time algorithms for this are known (for
instance one can triangulate the polygon then walk from triangle to
triangle); Paul Callahan discusses an alternate algorithm based on the
dynamic optimality conjecture for splay trees.
Line
designs for the computer. Jill Britton brings to the web material
from John Millington's 1989 book on geometric patterns formed by
stitching yarn through cardboard. The Java simulation of a Spectrum
computer running Basic programs is a little (ok a lot) clunky, and froze
Mozilla when I tried it, but there's also plenty of interesting static content.
Meru Foundation appears to be
another sacred geometry site, with animated gifs of torus knots
and other geometric visualizations and articles.
Mirrored room illumination.
A summary by Christine Piatko of the old open problem of, given
a polygon in which all sides are perfect mirrors, and a point source
of light, whether the entire polygon will be lit up.
The answer is no if smooth curves are allowed.
See also Eric Weisstein's page on the
Illumination
Problem.
A
new Masonic interpretation of Euclid's 47th Problem. Confused about
why those wacky Freemasons care so much about the Pythagorean Theorem,
Bro. Jeff Peace proposes the existence of a different Euclid
and a different 47th problem more related to theology than geometry.
New
perspective systems, by Dick Termes,
an artist who paints inside-out scenes on spheres which
give the illusion of looking into separate small worlds.
His site also includes an unfolded dodecahedron example
you can print, cut, and fold yourself.
Number patterns,
curves, and topology, J. Britton.
Includes sections on the golden ratio, conics, Moiré patterns,
Reuleaux triangles, spirograph curves, fractals, and flexagons.
Person polygons. Marc van Kreveld defines this interesting and
important class of simple polygons, and derives a linear time algorithm
(with a rather large constant factor) for recognizing a special case
in which there are many reflex vertices.
The
Perspective Page.
A short introduction to the geometry of perspective drawing.
Phaistos disk
geometry. Claire Watson examines the patterns on a Mediterranean
bronze-age artifact.
Plücker coordinates.
A description by Bob Knighten of this useful and standard way
of giving coordinates to lines, planes, and higher dimensional
subspaces of projective space.
Postscript
geometry.
Bill Casselman uses postscript to motivate a course
in Euclidean geometry.
See also his Coxeter group graph paper,
and Ed Rosten's
postscript doodles.
Beware, however, that postscript can not really represent
such basic geometric primitives as circles, instead approximating them
by splines.
Programming for 3d
modeling, T. Longtin. Tensegrity structures, twisted torus space frames,
Moebius band gear assemblies, jigsaw puzzle polyhedra, Hilbert fractal helices,
herds of turtles, and more.
Puzzles. Discussions on the geometry.puzzles list,
collected by topic at the Swarthmore Geometry Forum.
Quadrorhomb rotary engine
with chambers defined by the bars of a twelve-bar linkage rotating
around two nonconcentric axes.
Random polygons.
Tim Lambert summarizes responses to a request for
a good random distribution on the n-vertex simple polygons.
Sacred Geometry. Mystic insights into the
"principle of oneness underlying all geometry",
mixed with occasional outright falsehoods
such as the suggestion that dodecahedra and icosahedra arise in
crystals. But the illustrative diagrams are ok, if you just
ignore the words... For more mystic diagrams, see
The Sacred
Geometry Coloring Book.
Self-righting shapes.
Figures with only one stable and one unstable equilibrium, when placed
on a level surface. Surprisingly, they look much like certain kinds of turtles.
Julie J. Rehmeyer in MathTrek.
Shape metrics.
Larry Boxer and David Fry provide many bibliographic references
on functions measuring how similar two geometric shapes are.
Sighting point.
John McKay asks, given a set of co-planar points, how to find
a point to view them all from in a way that maximizes the
minimum viewing angle between any two points.
Somehow this is related to monodromy groups.
I don't know whether he ever got a useful response.
This is clearly
polynomial time: the decision problem can be solved by finding
the intersection of O(n2) shapes, each the union of two disks, so doing this
naively and applying parametric search gives O(n4 polylog),
but it might be interesting to push the time bound further.
A closely related problem of
smoothing a triangular mesh by moving points one at a time to
optimize the angles of incident triangles can be solved in linear time
by LP-type algorithms [Matousek, Sharir, and Welzl, SCG 1992;
Amenta, Bern, and Eppstein,
SODA 1997].
Smarandache
Manifolds online e-book by Howard Iseri.
I'm not sure I see why this should be useful or interesting, but the
idea seems to be to define geometry-like structures (having objects
called points and lines that somehow resemble Euclidean points and lines)
that are non-uniform in some strong sense: every Euclidean axiom
(and why not, every Euclidean theorem?) should be true at some point of
the geometry and false at some other point.
Squares on a Jordan curve.
Various people discuss the open problem of whether any Jordan curve
in the plane contains four points forming the vertices of a square,
and the related but not open problem of how to place
a square table level on a hilltop.
This is also in the
geometry.puzzles archive.
Splitting the hair.
Matthew Merzbacher discusses how many times one can subdivide
a line segment by following certain rules.
Subdivision
kaleidoscope. Strange diatom-like shapes formed by varying the
parameters of a spline surface mesh refinement scheme outside their
normal ranges.
Tic tac toe theorem.
Bill Taylor describes a construction of a warped
tic tac toe board from a given convex quadrilateral,
and asks for a proof that the middle quadrilateral
has area 1/9 the original. Apparently this is not
even worth a chocolate fish.
