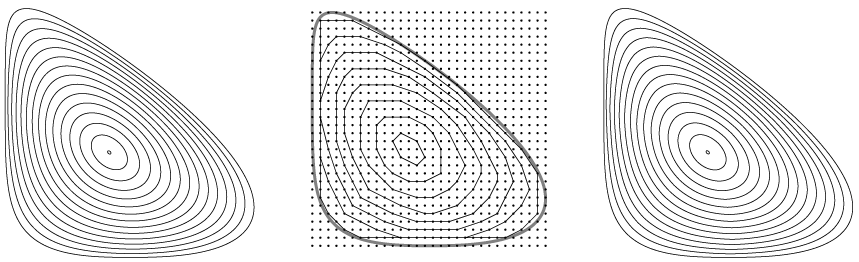
Peeling off the convex layers from the grid points inside a convex curve and applying the continuous affine curve-shortening flow to the curve seem to do the same thing. We don't understand why.
From a new arXiv preprint with +Sariel Har-Peled and +Gabriel Nivasch, https://arxiv.org/abs/1710.03960
Peeling vs shortening
I was surprised to see that we get nice smooth shapes even if we apply a square-shaped filter — but it is important here that the input is random and not adversarial.
I knew that there is a CA rule called "anneal" that behaves like the curve-shortening flow. See Wikipedia here:
However, for very small values of the window size it gets more boring: you will get fairly fine-grained structures and the process converges quickly. So something like 3x3 or 5x5 isn't that interesting yet.