ICS 1F, Homework 4 Solutions

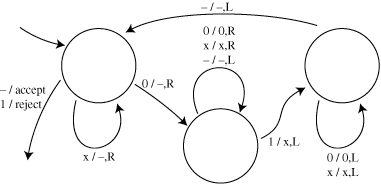
The circles in the following diagram represent the states of a Turing machine. An arrow labeled "a/b,D" means that if the machine sees the character "a", it replaces it by "b", moves in direction D (either left or right), and changes state as indicated by the arrow. An arrow labeled by "a/accept" or "a/reject" means the machine halts and accepts or rejects the string as indicated. The unlabeled arrow indicates the start state. A dash indicates the blank character.

1. Indicate for each of the following strings whether the machine above accepts, rejects, or goes into an infinite loop without halting: 01, 10, 011, 001, 0011.

   Note: there was a mistake in the Turing machine; the top arrow is supposed to be labeled "-/-,R" rather than "-/-,L". Other than this mistake, the machine is essentially the same as one for recognizing strings of balanced parentheses (but with the character zero instead of left parentheses and the character one instead of right parentheses). But because of this mistake, the problem was easier than it should have been.

   The answers for the machine given are that it rejects 10 and accepts all the other strings.

   The answers for the machine I intended to write are that it accepts 01 and 0011, rejects 10 and 011, and goes into a loop for 001.

2. Find a Turing machine that accepts strings of 0's and 1's only when the number of 1's is a power of two.

   (Hint: repeatedly pass left-to-right across the string to test whether there is exactly one "1" left, and right-to-left across the string changing every other "1" into a "0").

   

3. Why is it impossible to prove Church's thesis mathematically?

   Answer: because Church's thesis (namely, the idea that any computer we can actually build can be simulated by a Turing machine) is partially about the real world, and is therefore a statement of physics rather than purely mathematical. Physical theories can be disproven by experiments but can never be proven mathematically.