
ICS 180, Winter 1999:
Strategy and board game programming
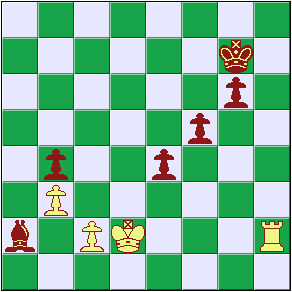
Here's an example. In the following position, black's bishop is trapped by the white pawns. No matter what black does, the bishop will be taken in a few moves; for instance the white rook could maneuver h2-h1-a1-a2 and capture the bishop. That sequence is 8 plys deep, and suppose that the black program is searching to a depth of 8 plys. Probably the best move for black in the actual position is to trade off the bishop and pawns, e.g. bishop x pawn, pawn x bishop. In the remaining endgame, black's three connected passed pawns may be enough to win or draw against the rook. But, a program searching 8 plys will likely instead move the black pawn forwards, checking the white king. White must respond (e.g. by taking the pawn with his king), but that forced response delays the loss of the bishop long enough that the program can't see it anymore, and thinks the bishop is safe. In fact, in this position, a fixed-depth program can continue throwing away its pawns, delaying the bishop capture a few more moves but probably causing the eventual loss of the game.

Shannon's original paper on computer chess listed two possible strategies for adjusting the search depth of a game program.
The most obvious is what the pseudo-code I've shown you so far does: a full-width, brute force search to a fixed depth. Just pass in a "depth" parameter to your program, decrement it by one for each level of search, and stop when it hits zero. This has the advantage of seeing even wierd-looking lines of play, as long as they remain within the search horizon. But the high branching factor means that it doesn't search any line very deeply (bachelor's degree: knows nothing about everything). And even worse, it falls prey to the horizon effect. Suppose, in chess, we have a program searching seven levels deep,
The other method suggested by Shannon was selective pruning: again search to some fixed depth, but to keep the branching factor down only search some of the children of each node (avoiding the "obviously bad" moves). So, it can search much more deeply, but there are lines it completely doesn't see (ph.d.: knows everything about nothing). Shannon thought this was a good idea because it's closer to how humans think. Turing used a variant of this idea, only searching capturing moves. More typically one might evaluate the children and only expand the k best of them where k is some parameter less than the true branching factor.
Unfortunately, "obviously bad" moves are often not bad at all, but are brilliant sacrifices that win the game. If you don't find one you should have made, you'll have to work harder and find some other way to win. Worse, if you don't see that your opponent is about to spring some such move sequence on you, you'll fall into the trap and lose.
Nowadays, neither of these ideas is used in its pure form. Instead, we use a synthesis of both: selective extension. We search all lines to some fixed depth, but then extend extend some lines deeper than that horizon. Sometimes we'll also do some pruning (beyond the safe pruning done by alpha-beta), but this is usually extremely conservative because it's too hard to pick out only the good moves; but we can sometimes pick out and ignore really bad moves. For games other than chess, with higher branching factors, it may be necessary to use more aggressive pruning techniques.
Quiescence search is the idea of, after reaching the main search horizon, running a Turing-like search in which we only expand capturing moves (or sometimes, capturing and checking) moves. For games other than chess, the main idea would be to only include moves which make large changes to the evaluation. Such a search must also include "pass" moves in which we decide to stop capturing. So, each call to the evaluation function in the main alpha-beta search would be replaced by the following, a slimmed down version of alpha-beta that only searches capturing moves, and that allows the search to stop if the current evaluation is already good enough for a fail high:
// quiescence search
// call this from the main alphabeta search in place of eval()
quiesce(int alpha, int beta) {
int score = eval();
if (score >= beta) return score;
for (each capturing move m) {
make move m;
score = -quiesce(-beta,-alpha);
unmake move m;
if (score >= alpha) {
alpha = score;
if (score >= beta) break;
}
}
return score;
}
Some people also include checks to the king inside the quiescence search,
but you have to be careful: because there is no depth parameter,
quiescence can search a huge number of nodes. Captures are naturally
limited (you can only perform 16 captures before you've run out of pieces
to capture) but checks can go on forever and cause an infinite recursion.
One trick helps make sure this extension idea terminate: only extend by a fraction of a level. Specifically, make the "depth" counter record some multiple of the number of levels you really want to search, say depth=levels*24. Then, in recursive calls to alpha-beta search, pass a value of depth-24+extension. If the extension is always strictly less than 24, the method is guaranteed to terminate, and you can choose which situations result in larger or smaller extensions.
It may also be useful to include within the evaluation function knowledge about how difficult a position is to evaluate, and extend the search on positions that are too difficult. My program does this: the program passes the current depth to the evaluation function. If the position is complicated, and the depth is close to zero, the evaluation returns a special value telling the search to continue. But if the depth reaches a large negative number, the evaluation function always succeeds, so that the search will eventually terminate.
The idea is based on a piece of knowledge about chess: it's very rare (except in the endgame) for it to be a disadvantage to move. Normally, if it's your turn to move, there is something you can do to make your position better. Positions in which all possible moves make the position worse are called "zugzwang" (German for move-compulsion), and normally only happen in endgames. In some other games, such as Go-Moku, zugzwang doesn't happen at all. So, if you changed the rules of chess to allow a "pass" move, passing would usually be a mistake and the game wouldn't change much.
So, suppose you have a search node that you expect to fail high (i.e., alphabeta will return a score of at least beta). The idea of null-move search is to search the "pass" move first, even though it's usually not the best move. If the pass move fails high, then the true best move is also likely to fail high, and you can return beta right away rather than searching it. To make this even faster, the depth at which the passing move is searched should be shallower than usual.
You should be careful: this heuristic changes the result of the search, and may cause you to miss some important lines of play. You shouldn't use null moves twice in a row (because then your search will degenerate to just returning the evaluation), and you should be careful to only use it in situations that are unlikely to be zugzwang. In chess, that means only positions with many pieces left.
// alpha-beta search with null-move heuristic
alphabeta(int depth, int alpha, int beta) {
if (won game or depth <= 0) return score;
make passing move;
if (last move wasn't null && position is unlikely to be zugzwang &&
-alphabeta(depth-3, -beta, -beta+1) >= beta)
return beta;
for (each possible move m) {
make move m;
alpha = max(alpha, -alphabeta(depth-1, -beta, -alpha);
unmake move m;
if (alpha >= beta) break;
}
return alpha;
}