Three-dimensional Geometry

• Adventures among the toroids. Reference to a book on polyhedral tori by B. M. Stewart.

• Antipodes. Jim Propp asks whether the two farthest apart points, as measured by surface distance, on a symmetric convex body must be opposite each other on the body. Apparently this is open even for rectangular boxes.

• Anton's modest little gallery of ray-traced 3d math.

• An aperiodic set of Wang cubes, J. UCS 1:10 (1995). Culik and Kari describe how to increase the dimension of sets of aperiodic tilings, turning a 13-square set of tiles into a 21-cube set.

• Aperiodic space-filling tiles: John Conway describes a way of glueing two prisms together to form a shape that tiles space only aperiodically. Ludwig Danzer speaks at NYU on various aperiodic 3d tilings including Conway's biprism.

• Art, Math, and Computers -- New Ways of Creating Pleasing Shapes, C. Séquin, Educator's TECH Exchange, Jan. 1996.

• Associahedron and Permutahedron. The associahedron represents the set of triangulations of a hexagon, with edges representing flips; the permutahedron represents the set of permutations of four objects, with edges representing swaps. This strangely asymmetric view of the associahedron (as an animated gif) shows that it has some kind of geometric relation with the permutahedron: it can be formed by cutting the permutahedron on two planes. A more symmetric view is below. See also a more detailed description of the associahedron and Jean-Louis Loday's paper on associahedron coordinates.

  

• Associating the symmetry of the Platonic solids with polymorf manipulatives.

• The Atomium, structure formed for Expo 1958 in the form of nine spheres, representing an iron crystal. The world's largest cube?

• David Bailey's world of tesselations. Primarily consists of Escher-like drawings but also includes an interesting section about Kepler's work on polyhedra.

• The bellows conjecture, R. Connelly, I. Sabitov and A. Walz in Contributions to Algebra and Geometry , volume 38 (1997), No.1, 1-10. Connelly had previously discovered non-convex polyhedra which are flexible (can move through a continuous family of shapes without bending or otherwise deforming any faces); these authors prove that in any such example, the volume remains constant throughout the flexing motion.

• Borromean rings don't exist. Geoff Mess relates a proof that the Borromean ring configuration (in which three loops are tangled together but no pair is linked) can not be formed out of circles. Dan Asimov discusses some related higher dimensional questions. Matthew Cook conjectures the converse.

  

• Bounded degree triangulation. Pankaj Agarwal and Sandeep Sen ask for triangulations of convex polytopes in which the vertex or edge degree is bounded by a constant or polylog.

• Box in a box. What is the smallest cube that can be put inside another cube touching all its faces? There is a simple solution, but it seems difficult to prove its correctness. The solution and proof are even prettier in four dimensions.

  

• Boy's surface: Wikipedia, MathWorld, Geometry Center, and an asymmetric animated gif from the Harvard zoo.

  

• Buckyballs. The truncated icosahedron recently acquired new fame and a new name when chemists discovered that Carbon forms molecules with its shape.

• The Cheng-Pleijel point. Given a closed plane curve and a height H, this point is the apex of the minimum surface area cone of height H over the curve. Ben Cheng demonstrates this concept with the help of a Java applet.

• Circumcenters of triangles. Joe O'Rourke, Dave Watson, and William Flis compare formulas for computing the coordinates of a circle's center from three boundary points, and higher dimensional generalizations.

• Circumnavigating a cube and a tetrahedron, Henry Bottomley.

• Cognitive Engineering Lab, Java applets for exploring tilings, symmetry, polyhedra, and four-dimensional polytopes.

• Collinear points on knots. Greg Kuperberg shows that a non-trivial knot or link in R³ necessarily has four colinear points.

  

• a computational approach to tilings. Daniel Huson investigates the combinatorics of periodic tilings in two and three dimensions, including a classification of the tilings by shapes topologically equivalent to the five Platonic solids.

• CSE logo. This java applet allows interactive control of a rotating collection of cubes.

• Cube Dissection. How many smaller cubes can one divide a cube into? From Eric Weisstein's treasure trove of mathematics.

• Cube triangulation. Can one divide a cube into congruent and disjoint tetrahedra? And without the congruence assumption, how many higher dimensional simplices are needed to triangulate a hypercube? For more on this last problem, see Triangulating an n-dimensional cube, S. Finch, MathSoft, and Asymptotically efficient triangulations of the d-cube, Orden and Santos.

  

• Curvature of knots. Steve Fenner proves the Fary-Milnor theorem that any smooth, simple, closed curve in 3-space must have total curvature at least 4 pi.

• Delta Blocks. Hop David discusses ideas for manufacturing building blocks based on the tetrahedron-octahedron space tiling depicted in Escher's "Flatworms".

• Deltahedra, polyhedra with equilateral triangle faces. From Eric Weisstein's treasure trove of mathematics.

• Densest packings of equal spheres in a cube, Hugo Pfoertner. With nice ray-traced images of each packing. See also Martin Erren's applet for visualizing the sphere packings.

  

• Dodecafoam. A fractal froth of polyhedra fills space.

• Dodecahedron measures, Paul Kunkel.

• Double bubbles. Joel Hass investigates shapes formed by soap films enclosing two separate regions of space.

• A dream about sphere kissing numbers.

• Edge-tangent polytope illustrating Koebe's theorem that any planar graph can be realized as the set of tangencies between circles on a sphere. Placing vertices at points having those circles as horizons forms a polytope with all edges tangent to the sphere. Rendered by POVray.

  

• Escher for real and beyond Escher for real. Gershon Elber uses layered manufacturing systems to build 3d models of Escher's illusions. The trick is to make some seemingly-flat surfaces curve towards and away from the viewplane.

  

• All the fair dice. Pictures of the polyhedra which can be used as dice, in that there is a symmetry taking any face to any other face.

• Fake dissection. An 8x8 (64 unit) square is cut into pieces which (seemingly) can be rearranged to form a 5x13 (65 unit) rectangle. Where did the extra unit come from? Jim Propp asks about possible three-dimensional generalizations. Greg Frederickson supplies one. See also Alexander Bogomolny's dissection of a 9x11 rectangle into a 10x10 square and Fibonacci bamboozlement applet.

  

• Figure eight knot / horoball diagram. Research of A. Edmonds into the symmetries of knots, relating them to something that looks like a packing of spheres. The MSRI Computing Group uses another horoball diagram as their logo.

• Filling space with unit circles. Daniel Asimov asks what fraction of 3-dimensional space can be filled by a collection of disjoint unit circles. (It may not be obvious that this fraction is nonzero, but a standard construction allows one to construct a solid torus out of circles, and one can then pack tori to fill space, leaving some uncovered gaps between the tori.) The geometry center has information in several places on this problem, the best being an article describing a way of filling space by unit circles (discontinuously).

• Five Platonic solids and a soccerball.

• Five space-filling polyhedra. And not the ones you're likely thinking of, either. Guy Inchbald, reproduced from Math. Gazette 80, November 1996.

• Flat equilateral tori. Can one build a polyhedral torus in which all faces are equilateral triangles and all vertices have six incident edges? Probably not but this physical model comes close.

  

• The flat torus in the three-sphere. Thomas Banchoff animates the Hopf fibration.

• Flatland: A Romance of Many Dimensions.

• Flexible polyhedra. From Dave Rusin's known math pages.

• Fractal broccoli. Photo by alfredo matacotta. See also this French page.

  

• Fun with Fractals and the Platonic Solids. Gayla Chandler places models of polyhedra and polyhedral fractals such as the Sierpinski tetrahedron in scenic outdoor settings and photographs them there.

• Gaussian continued fractions. Stephen Fortescue discusses some connections between basic number-theoretic algorithms and the geometry of tilings of 2d and 3d hyperbolic spaces.

• Geodesic dome design software. Now you too can generate triangulations of the sphere. Freeware for DOS, Mac, and Unix.

• Geometric Dissections by Gavin Theobald.

• The golden section and Euclid's construction of the dodecahedron, and more on the dodecahedron and icosahedron, H. Serras, Ghent.

• Gömböc, a convex body in 3d with a single stable and a single unstable point of equilibrium. Placed on a flat surface, it always rights itself; it may not be a coincidence that some tortoise shells are similarly shaped. See also Wikipedia, Metafilter, New York Times.

• Melinda Green's geometry page. Green makes models of regular sponges (infinite non-convex generalizations of Platonic solids) out of plastic "Polydron" pieces.

• Grid subgraphs. Jan Kristian Haugland looks for sets of lattice points that induce graphs with high degree but no short cycles.

• Hebesphenomegacorona onna stick in space! Space Station Science picture of the day. In case you don't remember what a hebesphenomegacorona is, it's one of the Johnson solids: convex polyhedra with regular-polygon faces.

• Hecatohedra. John Conway discusses the possible symmetry groups of hundred-sided polyhedra.

  

• Hedronometry. Don McConnell discusses equations relating the angles and face areas of tetrahedra. See also McConnell's hedronometry site.

• Helical geometry. Ok, renaming a hyperbolic paraboloid a "helical right triangle" and saying that it's "a revolutionary foundation for new knowledge" seems a little cranky but there are some interesting pictures of shapes formed by compounds of these saddles.

• Helical Gallery. Spirals in the work of M. C. Escher and in X-ray observations of the sun's corona.

• Heptomino Packings. Clive Tooth shows us all 108 heptominos, packed into a 7x9x12 box.

• Hilbert's 3rd Problem and Dehn Invariants. How to tell whether two polyhedra can be dissected into each other. See also Walter Neumann's paper connecting these ideas with problems of classifying manifolds.

• Hollow pyramid tetrasphere puzzle.

• Holyhedra. Jade Vinson solves a question of John Conway on the existence of finite polyhedra all of whose faces have holes in them (the Menger sponge provides an infinite example).

• How many points can one find in three-dimensional space so that all triangles are equilateral or isosceles? One eight-point solution is formed by placing three points on the axis of a regular pentagon. This problem seems related to the fact that any planar point set forms O(n^7/3) isosceles triangles; in three dimensions, Theta(n³) are possible (by generalizing the pentagon solution above). From Stan Wagon's PotW archive.

• Human Geometry and Naked Geometry. The human form as a building block of larger geometric figures, by Mike Naylor.

• Ideal hyperbolic polyhedra ray-traced by Matthias Weber.

• Guy Inchbald's polyhedra pages. Stellations, hendecahedra, duality, space-fillers, quasicrystals, and more.

• IFS and L-systems. Vittoria Rezzonico grows fractal broccoli and Sierpinski pyramids.

• Interactive fractal polyhedra, Evgeny Demidov.

• The International Bone-Roller's Guild ponders the isohedra: polyhedra that can act as fair dice, because all faces are symmetric to each other.

• Intersecting cube diagonals. Mark McConnell asks for a proof that, if a convex polyhedron combinatorially equivalent to a cube has three of the four body diagonals meeting at a point, then the fourth one meets there as well. There is apparently some connection to toric varieties.

• Java lamp, S. M. Christensen.

• Johnson Solids, convex polyhedra with regular faces. From Eric Weisstein's treasure trove of mathematics.

• Sándor Kabai's mathematical graphics, primarily polyhedra and 3d fractals.

• Aaron Kellner Linear Sculpture. Art in the form of geometric tangles of metal and wood rods.

• Kelvin conjecture counterexample. Evelyn Sander forwards news about the discovery by Phelan and Weaire of a better way to partition space into equal-volume low-surface-area cells. Kelvin had conjectured that the truncated octahedron provided the optimal solution, but this turned out not to be true. See also Ruggero Gabbrielli's comparison of equal-volume partitions and JavaView foam models.

  

• Kepler-Poinsot Solids, concave polyhedra with star-shaped faces. From Eric Weisstein's treasure trove of mathematics. See also H. Serras' page on Kepler-Poinsot solids.

• Knot pictures. Energy-minimized smooth and polygonal knots, from the ming knot evolver, Y. Wu, U. Iowa.

• Mathematical imagery by Jos Leys. Knots, Escher tilings, spirals, fractals, circle inversions, hyperbolic tilings, Penrose tilings, and more.

• Louis Bel's povray galleries: les polyhèdres réguliers, knots, and more knots.

• Maille Weaves. Different repetitive patterns formed by linked circles along a plane in space, as used for making chain mail. Along with some linear patterns for jewelry chains.

• Maple polyhedron gallery.

• Martin's pretty polyhedra. Simulation of particles repelling each other on the sphere produces nice triangulations of its surface.

• Mathematica Graphics Gallery: Polyhedra

• Mathenautics. Visualization of 3-manifold geometry at the Univ. of Illinois.

• MatHSoliD Java animation of planar unfoldings of the Platonic and Archimedean polyhedra.

• Minesweeper on Archimedean polyhedra, Robert Webb.

• Minimax elastic bending energy of sphere eversions. Rob Kusner, U. Mass. Amherst.

• Minimizing surface area to volume ratio in a cube.

• Maximum volume arrangements of points on a sphere, Hugo Pfoertner.

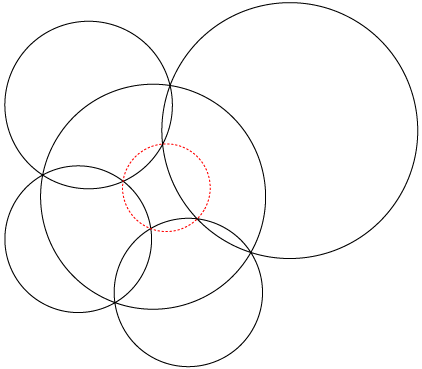
• Miquel's six circles in 3d. Reinterpreting a statement about intersecting circles to be about inscribed cuboids.

  

• Modeling mollusc shells with logarithmic spirals, O. Hammer, Norsk Net. Tech. Also includes a list of logarithmic spiral links.

• Models of Platonic solids and related symmetric polyhedra.

• Nested Klein bottles. From the London Science Museum gallery, by way of Boing Boing. Topological glassware by Alan Bennett.

  

• Netlib polyhedra. Coordinates for regular and Archimedean polyhedra, prisms, anti-prisms, and more.

• Nine. Drew Olbrich discovers the associahedron by evenly spacing nine points on a sphere and dualizing.

• No cubed cube. David Moews offers a cute proof that no cube can be divided into smaller cubes, all different.

• T. Nordstrand's gallery of surfaces.

• Not. AMS Cover, Apr. 1995. This illustration for an article on geometric tomography depicts objects (a cuboctahedron and warped rhombic dodecahedron) that disguise themselves as regular tetrahedra by having the same width function or x-ray image.

• Objects that cannot be taken apart with two hands. J. Snoeyink, U. British Columbia.

• Occult correspondences of the Platonic solids. Some random thoughts from Anders Sandberg.

• Orthogonal discrete knots. Hew Wolff asks questions about the minimum total length, or the minimum volume of a rectangular box, needed to form different knots as three-dimensional polygons using only integer-length axis-parallel edges.

• Packing circles in circles and circles on a sphere, Jim Buddenhagen. Mostly about optimal packing but includes also some nonoptimal spiral and pinwheel packings.

• Packing Tetrahedrons, and Closing in on a Perfect Fit. Elizabeth Chen and others use experiments on hundreds of D&D dice to smash previous records for packing density.

• Pairwise touching hypercubes. Erich Friedman asks how to partition the unit cubes of an a*b*c-unit rectangular box into as many connected polycubes as possible with a shared face between every pair of polycubes. He lists both general upper and lower bounds as functions of a, b, and c, and specific constructions for specific sizes of box. I've seen the same question asked for d-dimensional hypercubes formed out of 2^d unit hypercubes; there is a lower bound of roughly 2^d/2 (from embedding a 2*2^d/2*2^d/2 box into the hypercube) and an upper bound of O(2^d/2 sqrt d) (from computing how many cubes must be in a polycube to give it enough faces to touch all the others).

• Pappus on the Archimedean solids. Translation of an excerpt of a fourth century geometry text.

• Penumbral shadows of polygons form projections of four-dimensional polytopes. From the Graphics Center's graphics archives.

• Pictures of 3d and 4d regular solids, R. Koch, U. Oregon. Koch also provides some 4D regular solid visualization applets.

• The Platonic solids. With Java viewers for interactive manipulation. Peter Alfeld, Utah.

• Platonic solids and Euler's formula. Vishal Lama shows how the formula can be used to show that the familiar five Platonic solids are the only ones possible.

• Platonic solids transformed by Michael Hansmeyer using subdivision-surface algorithms into shapes resembling radiolarans. See also Boing Boing discussion.

• Platonic Universe, Stephan Werbeck. What shapes can you form by gluing regular dodecahedra face-to-face?

• Polygons as projections of polytopes. Andrew Kepert answers a question of George Baloglou on whether every planar figure formed by a convex polygon and all its diagonals can be formed by projecting a three-dimensional convex polyhedron.

• Polyhedra. Bruce Fast is building a library of images of polyhedra. He describes some of the regular and semi-regular polyhedra, and lists names of many more including the Johnson solids (all convex polyhedra with regular faces).

• Polyhedra Blender. Mathematica software and Java-based interactive web gallery for what look like Minkowski sums of polyhedra. If the inputs to the Minkowski sums were line segments, cubes, or zonohedra, the results would be again zonohedra, but the ability to supply other inputs allows more general polyhedra to be formed.

• Polyhedra collection, V. Bulatov.

• Polyhedra exhibition. Many regular-polyhedron compounds, rendered in povray by Alexandre Buchmann.

• A polyhedral analysis. Ken Gourlay looks at the Platonic solids and their stellations.

• Polyhedron, polyhedra, polytopes, ... - Numericana.

• Polyhedron challenge: cuboctahedron.

• Polyominoids, connected sets of squares in a 3d cubical lattice. Includes a Java applet as well as non-animated description. By Jorge L. Mireles Jasso.

• The Pretzel Page. Eric Sedgwick uses animated movies of twisting pretzel knots to visualize a theorem about Heegard splittings (ways of dividing a complex topological space into two simple pieces).

• Prince Rupert's Cube. It's possible to push a larger cube through a hole drilled into a smaller cube. How much larger? 1.06065... From Eric Weisstein's treasure trove of mathematics.

• Prince Rupert's tetrahedra? One tetrahedron can be entirely contained in another, and yet have a larger sum of edge lengths. But how much larger? From Stan Wagon's PotW archive.

• Programming for 3d modeling, T. Longtin. Tensegrity structures, twisted torus space frames, Moebius band gear assemblies, jigsaw puzzle polyhedra, Hilbert fractal helices, herds of turtles, and more.

• Proofs of Euler's Formula. V-E+F=2, where V, E, and F are respectively the numbers of vertices, edges, and faces of a convex polyhedron.

• Pseudospherical surfaces. These surfaces are equally "saddle-shaped" at each point.

• Quaquaversal Tilings and Rotations. John Conway and Charles Radin describe a three-dimensional generalization of the pinwheel tiling, the mathematics of which is messier due to the noncommutativity of three-dimensional rotations.

• Quark constructions. The sun4v.qc Team investigates polyhedra that fit together to form a modular set of building blocks.

• Quark Park. An ephemeral outdoor display of geometric art, in Princeton, New Jersey. From Ivars Peterson's MathTrek.

  Quasicrystals and aperiodic tilings, A. Zerhusen, U. Kentucky. Includes a nice description of how to make 3d aperiodic tiles from zometool pieces.

• Qubits, modular geometric building blocks by architect Mark Burginger, inspired by Fuller's geodesic domes.

• Ram's Horn cardboard model of an interesting 3d spiral shape bounded by a helicoid and two nested cones.

• Regard mathématique sur Bruxelles. Student project to photograph city features of mathematical interest and model them in Cabri.

• Regular polyhedra as intersecting cylinders. Jim Buddenhagen exhibits ray-traces of the shapes formed by extending half-infinite cylinders around rays from the center to each vertex of a regular polyhedron. The boundary faces of the resulting unions form combinatorially equivalent complexes to those of the dual polyhedra.

• Regular solids. Information on Schlafli symbols, coordinates, and duals of the five Platonic solids. (This page's title says also Archimedean solids, but I don't see many of them here.)

• Rhombic spirallohedra, concave rhombus-faced polyhedra that tile space, R. Towle.

• Riemann Surfaces and the Geometrization of 3-Manifolds, C. McMullen, Bull. AMS 27 (1992). This expository (but very technical) article outlines Thurston's technique for finding geometric structures in 3-dimensional topology.

• Rob's polyhedron models, made with the help of his program Stella.

• Robinson Friedenthal polyhedral explorations. Geometric sculpture.

• Rolling polyhedra. Dave Boll investigates Hamiltonian paths on (duals of) regular polyhedra.

• Rudin's example of an unshellable triangulation. In this subdivision of a big tetrahedron into small tetrahedra, every small tetrahedron has a vertex interior to a face of the big tetrahedron, so you can't remove any of them without forming a hole. Peter Alfeld, Utah.

• Ruler and Compass. Mathematical web site including special sections on the geometry of polyhedrons and geometry of polytopes.

• The Schläfli Double Six. A lovely photo-essay of models of this configuration, in which twelve lines each meet five of thirty points. Unfortunately only the first page seems to be archived... (This site also referred to related configurations involving 27 lines meeting either 45 or 135 points, but didn't describe any mathematical details. For further descriptions of all of these, see Hilbert and Cohn-Vossen's "Geometry and the Imagination".)

• In search of the ideal knot. Piotr Pieranski applies an iterative shrinking heuristic to find the minimum length unit-diameter rope that can be used to tie a given knot.

• Seashell spirals. Xah Lee examines the shapes of various real seashells, and offers prize money for formulas duplicating them.

• The Sierpinski Tetrahedron, everyone's favorite three dimensional fractal. Or is it a fractal?

• SingSurf software for calculating singular algebraic curves and surfaces, R. Morris.

• Six-regular toroid. Mike Paterson asks whether it is possible to make a torus-shaped polyhedron in which exactly six equilateral triangles meet at each vertex.

• Skewered lines. Jim Buddenhagen notes that four lines in general position in R³ have exactly two lines crossing them all, and asks how this generalizes to higher dimensions.

• Soap films on knots. Ken Brakke, Susquehanna.

• Soddy's Hexlet, six spheres in a ring tangent to three others, and Soddy's Bowl of Integers, a sphere packing combining infinitely many hexlets, from Mathworld.

• Solution of Conway-Radin-Sadun problem. Dissections of combinations of regular dodecahedra, regular icosahedra, and related polyhedra into rhombs that tile space. By Dehn's solution to Hilbert's third problem this is impossible for individual dodecahedra and icosahedra, but Conway, Radin, and Sadun showed that certain combinations could work. Now Izidor Hafner shows how.

• Solution to problem 10769. Apparently problems of coloring the points of a sphere so that orthogonal points have different colors (or so that each set of coordinate basis vectors has multiple colors) has some relevance to quantum mechanics; see also papers quant-ph/9905080 and quant-ph/9911040 (on coloring just the rational points on a sphere), as well as this four-dimensional construction of an odd number of basis sets in which each vector appears an even number of times, showing that one can't color the points on a four-sphere so that each basis set has exactly one black point.

• Soma cube applet.

• The soma cube page and pentomino page, J. Jenicek.

• Some images made by Konrad Polthier.

• Some pictures of symmetric tensegrities.

• SpaceBric building blocks and Windows software based on a tiling of 3d space by congruent tetrahedra.

• Sphere packing and kissing numbers. How should one arrange circles or spheres so that they fill space as densely as possible? What is the maximum number of spheres that can simultanously touch another sphere?

• Spherical Julia set with dodecahedral symmetry discovered by McMullen and Doyle in their work on quintic equations and rendered by Don Mitchell. Update 12/14/00: I've lost the big version of this image and can't find DonM anywhere on the net -- can anyone help? In the meantime, here's a link to McMullen's rendering.

  

• The sphericon, a convex shape with one curved face and two semicircular edges that can roll with a wobbling motion in a straight line. See also the national curve bank sphericon page, the MathWorld sphericon page, the Wikipedia sphericon page, The Differential Geometry of the Sphericon, and building a sphericon.

• Spiral tower. Photo of a building in Iraq, part of a web essay on the geometry of cyberspace.

• Spiraling Sphere Models. Bo Atkinson studies the geometry of a solid of revolution of an Archimedean spiral.

• Spring into action. Dynamic origami. Ben Trumbore, based on a model by Jeff Beynon from Tomoko Fuse's book Spirals.

• Square Knots. This article by Brian Hayes for American Scientist examines how likely it is that a random lattice polygon is knotted.

• Stella and Stella4d, Windows software for visualizing regular and semi-regular polyhedra and their stellations in three and four dimensions, morphing them into each other, drawing unfolded nets for making paper models, and exporting polyhedra to various 3d design packages.

• Sterescopic polyhedra rendered with POVray by Mark Newbold.

• Steve's sprinklers. An interesting 3d polygon made of copper pipe forms various symmetric 2d shapes when viewed from different directions.

• Subdivision kaleidoscope. Strange diatom-like shapes formed by varying the parameters of a spline surface mesh refinement scheme outside their normal ranges.

• Symmetries of torus-shaped polyhedra

• The Szilassi Polyhedron. This polyhedral torus, discovered by L. Szilassi, has seven hexagonal faces, all adjacent to each other. It has an axis of 180-degree symmetry; three pairs of faces are congruent leaving one unpaired hexagon that is itself symmetric. Tom Ace has more images as well as a downloadable unfolded pattern for making your own copy. See also Dave Rusin's page on polyhedral tori with few vertices and Ivars' Peterson's MathTrek article.

  

• Tales of the dodecahedron, from Pythagoras to Plato to Poincaré. John Baez, Reese Prosser Memorial Lecture, Dartmouth, 2006.

• Tangencies of circles and spheres. E. F. Dearing provides formulae for the radii of Apollonian circles, and analogous three-dimensional problems.

• Tensegrity zoology. A catalog of stable structures formed out of springs, somehow forming a quantum theory of what used to be described as time.

• Tetrahedra packing. Mathematica implementation of the Chen-Engel-Glotzer packing of space by regular tetrahedra, the densest known such packing to date.

• Tetrahedrons and spheres. Given an arbitrary tetrahedron, is there a sphere tangent to each of its edges? Jerzy Bednarczuk, Warsaw U.

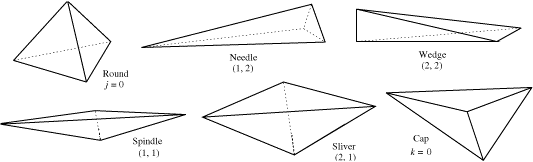
• Tetrahedra classified by their bad angles. From "Dihedral bounds for mesh generation in high dimensions".

  

• These two pictures by Richard Phillips are from the now-defunct maths with photographs website. The chimney is (Phillips thinks) somewhere in North Nottinghamshire, England. A similar collection of Phillips' mathematical photos is now available on CD-ROM.

     

• Thoughts on the number six. John Baez contemplates the symmetries of the icosahedron.

• Three cubes to one. Calydon asks whether nine pieces is optimal for this dissection problem.

• 3D-Geometrie. T. E. Dorozinski provides a gallery of images of 3d polyhedra, 2d and 3d tilings, and subdivisions of curved surfaces.

• 3d-XplorMath Macintosh software for visualizing curves, surfaces, polyhedra, conformal maps, and other planar and three-dimensional mathematical objects.

• Three-dimensional models based on the works of M. C. Escher

• The three dimensional polyominoes of minimal area, L. Alonso and R. Cert, Elect. J. Combinatorics.

• Three dimensional turtle talk description of a dodecahedron. The dodecahedron's description is "M40T72R5M40X63.435T288X296.565R5M40T72M40X63.435T288X296.565R4"; isn't that helpful?

• 3D strange attractors and similar objects, Tim Stilson, Stanford.

• Three untetrahedralizable objects

     

• Tilable perspectives. Patrick Snels creates two-dimensional images which tile the plane to form 3d-looking views including some interesting Escher-like warped perspectives. See also his even more Escherian tesselations page.

• Tiling with four cubes. Torsten Sillke summarizes results and conjectures on the problem of tiling 3-dimensional boxes with a tile formed by gluing three cubes onto three adjacent faces of a fourth cube.

• Tiling with notched cubes. Robert Hochberg and Michael Reid exhibit an unboxable reptile: a polycube that can tile a larger copy of itself, but can't tile any rectangular block.

• Toroidal tile for tessellating three-space, C. Séquin, UC Berkeley.

• Triangulating 3-dimensional polygons. This is always possible (with exponentially many Steiner points) if the polygon is unknotted, but NP-complete if no Steiner points are allowed. The proof uses gadgets in which quadrilaterals are stacked like Pringles to form wires.

  

• Triangulation numbers. These classify the geometric structure of viruses. Many viruses are shaped as simplicial polyhedra consisting of 12 symmetrically placed degree five vertices and more degree six vertices; the number represents the distance between degree five vertices.

• Triply orthogonal surfaces, Matthias Weber.

• Truncated Octahedra. Hop David has a nice picture of Coxeter's regular sponge {6,4|4}, formed by leaving out the square faces from a tiling of space by truncated octahedra.

• Truncated Trickery: Truncatering. Some truncation relations among the Platonic solids and their friends.

• Tune's polyhedron models. Sierpinski octahedra, stellated icosahedra, interlocking zonohedron-dissection puzzles, and more.

• Turkey stuffing. A cube dissection puzzle from IBM research.

• Tuvel's Polyhedra Page and Tuvel's Hyperdimensional Page. Information and images on universal polyhedra and higher dimensional polytopes.

• 27 lines on the Clebsch cubic, Matthias Weber.

• The uniform net (10,3)-a. An interesting crystal structure formed by packing square and octagonal helices.

• Uniform polyhedra. Computed by Roman Maeder using a Mathematica implementation of a method of Zvi Har'El. Maeder also includes separately a picture of the 20 convex uniform polyhedra, and descriptions of the 59 stellations of the icosahedra.

• Uniform polyhedra in POV-ray format, by Russell Towle.

  

• Uniform polyhedra, R. Morris. Rotatable 3d java view of these polyhedra.

• An uninscribable 4-regular polyhedron. This shape can not be drawn with all its vertices on a single sphere.

  

• Visualization of the Carrillo-Lipman Polytope. Geometry arising from the simultaneous comparison of multiple DNA or protein sequences.

• Volume of a torus. Paul Kunkel describes a simple and intuitive way of finding the formula for a torus's volume by relating it to a cylinder.

• Volumes in synergetics. Volumes of various regular and semi-regular polyhedra, scaled according to inscribed tetrahedra.

• Volumes of pieces of a dodecahedron. David Epstein (not me!) wonders why parallel slices through the layers of vertices of a dodecahedron produce equal-volume chunks.

• vZome zometool design software for OS X and Windows. (Warning, web site may be down on off-hours.)

• The Water Cube swimming venue at the 2008 Beijing Olympics uses the Weaire-Phelan foam (a partition of 3d space into equal-volume cells with the minimum known surface area per unit volume) as the basis of its structure.

  

• Waterman polyhedra, formed from the convex hulls of centers of points near the origin in an alternating lattice. See also Paul Bourke's Waterman Polyhedron page.

  

• Matthias Weber's gallery of ray-traced mathematical objects, such as minimal surfaces floating in ponds.

• Why doesn't Pick's theorem generalize? One can compute the volume of a two-dimensional polygon with integer coordinates by counting the number of integer points in it and on its boundary, but this doesn't work in higher dimensions.

• Why "snub cube"? John Conway provides a lesson on polyhedron nomenclature and etymology. From the geometry.research archives.

• Zometool. The 31-zone structural system for constructing "mathematical models, from tilings to hyperspace projections, as well as molecular models of quasicrystals and fullerenes, and architectural space frame structures".

• Zonohedra and zonotopes. These centrally symmetric polyhedra provide another way of understanding the combinatorics of line arrangements.

• A zoo of surfaces.

• Frank Zubek's Elusive Cube. Magnetic tetrahedra connect to form dissections of cubes and many other shapes.